题目内容
5.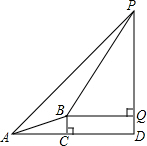 如图,某校综合实践活动小组同学欲测量台阶平台上电线杆PQ的高度,他们在台阶下A点处测得电线杆顶端P的仰角∠PAC为45°,沿着台阶走到台阶上的点B处,测得电线杆顶端P的仰角∠PBQ为57°,已知BC的高度为2m,台阶AB的坡比为1:3,BQ∥AC,求电线杆PQ的高度.(参考数据:tan57°≈$\frac{3}{2}$,sin57°≈$\frac{4}{5}$)
如图,某校综合实践活动小组同学欲测量台阶平台上电线杆PQ的高度,他们在台阶下A点处测得电线杆顶端P的仰角∠PAC为45°,沿着台阶走到台阶上的点B处,测得电线杆顶端P的仰角∠PBQ为57°,已知BC的高度为2m,台阶AB的坡比为1:3,BQ∥AC,求电线杆PQ的高度.(参考数据:tan57°≈$\frac{3}{2}$,sin57°≈$\frac{4}{5}$)
分析 根据台阶AB的坡比为1:3,求出BC=2,从而表示出AD的长,再表示出PQ的长,Rt△PBQ中,$\frac{4+x}{x}$=tan57°,求出x的长,从而求出PQ的长.
解答 解:∵台阶AB的坡比为1:3,BC=2,
∴AC=6,
设CD=xm,
则AD=(6+x)m,
∵∠PAC=45°,
∴PD=AD=(6+x)m,PQ=6+x-2=(4+x)m,
在Rt△PBQ中,$\frac{4+x}{x}$=tan57°,
即$\frac{4+x}{x}$≈$\frac{3}{2}$,
解得,x=8.,
∴PQ=BQ•tan57°≈8×$\frac{3}{2}$=12m.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
15.在△ABC中,AB2=2BC2,AC=BC,那么∠A:∠B:∠C为( )
| A. | 1:2:3 | B. | 2:1:3 | C. | 1:1:2 | D. | 1:2:1 |
16.2015年羊年除夕夜的10点半,在央视春晚送红包的活动中,微信“摇一摇”峰值的摇动次数达到8.1亿次/分钟,送出微信红包120 000 000个.将120 000 000用科学记数法表示应为( )
| A. | 0.12×109 | B. | 1.2×107 | C. | 1.2×108 | D. | 12×107 |
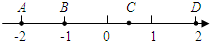 如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )
如图,数轴上用点A,B,C,D表示有理数,下列语句正确的有( )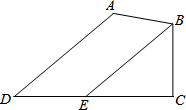 已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.