题目内容
14.方程组$\left\{\begin{array}{l}{2x+y=3}\\{3x-z=7}\\{x-y+3z=0}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=1}\end{array}\right.$ |
分析 由②③消去z,转化为二元方程组即可解决问题.
解答 解:$\left\{\begin{array}{l}{2x+y=3}&{①}\\{3x-z=7}&{②}\\{x-y+3z=0}&{③}\end{array}\right.$
②×3+③得到:10x-y=21 ④
由①④解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$代入②得z=-1,
∴$\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=-1}\end{array}\right.$,
故选C.
点评 本题考查三元方程组,解题的关键是三元方程组转化为二元方程组,学会转化的数学思想,属于中考常考题型.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
19.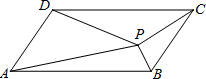 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A. | S1+S2=S3+S4 | B. | S1+S2>S3+S4 | C. | S1+S3=S2+S4 | D. | S1+S2<S3+S4 |
6.①对顶角相等;②两点之间线段最短;③相等的角是对顶角;④同位角相等.其中假命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
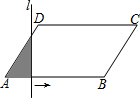 如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.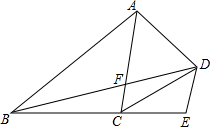 四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.
四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.