题目内容
阅读
=
=
=
-1
=2-
,…,观察上面结果,直接写出
= .利用以上提供的方法化简下式:
+
+
+…+
.
| 1 | ||
1+
|
| ||||||
(
|
| ||
| 2-1 |
| 2 |
| 1 | ||||
|
| 3 |
| 1 | ||||
|
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
考点:分母有理化
专题:规律型
分析:根据观察,可发现规律:
=
-
,根据规律,可分母有理化,根据二次根式的加减,可得答案.
| 1 | ||||
|
| n+1 |
| n |
解答:解:由等式,得
=
-
,
故答案为:
-
,
+
+
+…+
=
-1+
-
+
-
+…+
-
=
-1
=10-1
=9.
| 1 | ||||
|
| n+1 |
| n |
故答案为:
| n+1 |
| n |
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 100 |
| 99 |
=
| 100 |
=10-1
=9.
点评:本题考查了分母有理化,根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
下列说法不成立的是( )
| A、若两图形关于某直线对称,那么对称轴是对应点连线的中垂线 |
| B、两图形若关于某直线对称,则两图形能重合 |
| C、等腰三角形是轴对称图形 |
| D、线段的对称轴只有一条 |
 如图,以下结论中正确的是( )
如图,以下结论中正确的是( )| A、AB+AC>BC |
| B、AB+AC=BC |
| C、AB+AC<BC |
| D、不能确定 |
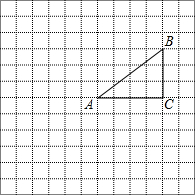 如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点.
如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点.
 如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )
如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )