题目内容
用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:
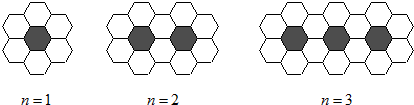
(1)当黑砖n=1时,白砖有 块,当黑砖n=2时,白砖有 _块,
(2)第n个图案中,白色地砖共 块.
(3)第几个图形有2014块白色地砖?请说明理由.
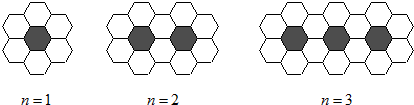
(1)当黑砖n=1时,白砖有
(2)第n个图案中,白色地砖共
(3)第几个图形有2014块白色地砖?请说明理由.
考点:规律型:图形的变化类
专题:
分析:(1)第1个图里有白色地砖6+4(1-1)=6;第2个图里有白色地砖6+4(2-1)=10;第3个图里有白色地砖6+4(3-1)=14;…;
(2)由(1)得出第n个图里有白色地砖6+4(n-1)=4n+2;
(3)将2014代入求得n的数值即可.
(2)由(1)得出第n个图里有白色地砖6+4(n-1)=4n+2;
(3)将2014代入求得n的数值即可.
解答:解:∵每个图形都比其前一个图形多4个白色地砖,
∴可得规律为:第n个图形中有白色地砖6+4(n-1)=(4n+2)块;
(1)第1个图里有白色地砖6+4(1-1)=6块;第2个图里有白色地砖6+4(2-1)=10块;
(2)第n个图里有白色地砖6+4(n-1)=4n+2块;
(3)4n+2=2014
解得n=503
所以第503个图形有2014块白色地砖.
故答案为:(1)6,10;(2)4n+2.
∴可得规律为:第n个图形中有白色地砖6+4(n-1)=(4n+2)块;
(1)第1个图里有白色地砖6+4(1-1)=6块;第2个图里有白色地砖6+4(2-1)=10块;
(2)第n个图里有白色地砖6+4(n-1)=4n+2块;
(3)4n+2=2014
解得n=503
所以第503个图形有2014块白色地砖.
故答案为:(1)6,10;(2)4n+2.
点评:此题考查图形的变化规律,重点考查了通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
相关题目
若a=-32,b=-|-2|,c=(-2)3,则( )
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
若⊙O所在平面内一点P到⊙O上的点的最大距离为7,最小距离为3,则此圆的半径为( )
| A、5 | B、2 | C、10或4 | D、5或2 |
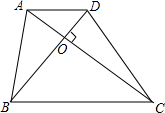 如图所示已知梯形ABCD中,AD∥BC,BD=6,AC=8,AC⊥BD于O,
如图所示已知梯形ABCD中,AD∥BC,BD=6,AC=8,AC⊥BD于O,