题目内容
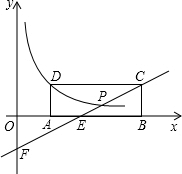 如图,矩形ABCD在第一象限,AB在x轴正半轴上;AB=m,BC=1,直线y=
如图,矩形ABCD在第一象限,AB在x轴正半轴上;AB=m,BC=1,直线y=| 1 |
| 2 |
| k |
| x |
| 3 |
(1)求k的值;
(2)求点C的坐标;
(3)m为多少时,双曲线y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将P点的坐标代入直线y=
x-1中即可求得P点的坐标,然后代入双曲线y=
(x>0)中,就可以求得k的值,
(2)由于BC=1,即C点的纵坐标为1,利用直线y=
x-1可确定C点坐标为(4,1).
(3)根据题意D点的坐标为(4-m,1),代入y=
即可求得m的值.
| 1 |
| 2 |
| k |
| x |
(2)由于BC=1,即C点的纵坐标为1,利用直线y=
| 1 |
| 2 |
(3)根据题意D点的坐标为(4-m,1),代入y=
| 1 |
| x |
解答:解:(1)∵直线y=
x-1过P(
+1,n),
∴n=
(
+1)-1=
∴P(
+1,
),
双曲线y=
(x>0)过P点,
∴
+1=
,
∴k=1,
∴y=
(x>0).
(2)根据矩形的性质知点C的纵坐标是y=1,
∵y=
x-1经过点C,
∴1=
x-1,
解得,x=4,
即点C的坐标是(4,1).
(3)由(2)可知D点的坐标为(4-m,1),
∵双曲线y=
经过点D(4-m,1),
∴1=
,
解得m=3,
即m=3时双曲线y=
(x>0)经过点D.
| 1 |
| 2 |
| 3 |
∴n=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴P(
| 3 |
| ||
| 2 |
双曲线y=
| k |
| x |
∴
| 3 |
| k | ||||
|
∴k=1,
∴y=
| 1 |
| x |
(2)根据矩形的性质知点C的纵坐标是y=1,
∵y=
| 1 |
| 2 |
∴1=
| 1 |
| 2 |
解得,x=4,
即点C的坐标是(4,1).
(3)由(2)可知D点的坐标为(4-m,1),
∵双曲线y=
| 1 |
| x |
∴1=
| 1 |
| 4-m |
解得m=3,
即m=3时双曲线y=
| 1 |
| x |
点评:本题考查了一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征.解题时,利用了“矩形的对边相等,四个角都是直角的性质.

练习册系列答案
相关题目
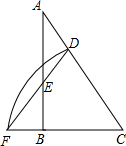 如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC=
如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC=
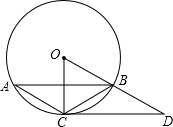 如图,已知△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°.
如图,已知△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°.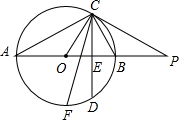 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB. 如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.
如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.