题目内容
2.先化简,再求值:$\frac{(x-2)(x+3)}{{{x^2}-9}}•\frac{x-3}{{{x^2}-2x}}$,其中x=-2.分析 先把分子分母因式分解,然后约分得到原式=$\frac{1}{x}$,再把x的值代入计算即可.
解答 解:原式=$\frac{(x-2)(x+3)}{(x+3)(x-3)}$•$\frac{x-3}{x(x-2)}$
=$\frac{1}{x}$
当x=-2时,原式=$\frac{1}{2}$.
点评 分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.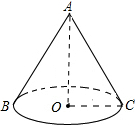 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )| A. | 9π | B. | 24π | C. | 15π | D. | 30π |
14.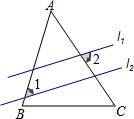 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )| A. | 45° | B. | 55° | C. | 80° | D. | 100° |
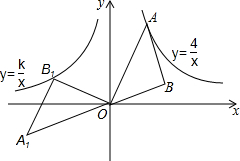 如图,A是反比例函数y=$\frac{4}{x}$(x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=$\frac{k}{x}$的图象经过点B1,则k的值是-2.
如图,A是反比例函数y=$\frac{4}{x}$(x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=$\frac{k}{x}$的图象经过点B1,则k的值是-2.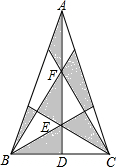 如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是6.
如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是6.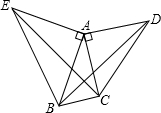 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问: