若a1=1-$\frac{1}{m}$.a2=1-$\frac{1}{{a} {1}}$.a3=1-$\frac{1}{{a} {2}}$.-,则a2013的值为m．题目和参考答案——青夏教育精英家教网—

题目内容

10．若a₁=1-$\frac{1}{m}$，a₂=1-$\frac{1}{{a}_{1}}$，a₃=1-$\frac{1}{{a}_{2}}$，…；则a₂₀₁₃的值为m．（用含m的代数式表示）

分析把a₁代入求出a₂，把a₂代入求出a₃，依此类推得到一般性规律，即可确定出所求式子的值．

解答解：a₁=1-$\frac{1}{m}$，a₂=1-$\frac{1}{{a}_{1}}$=1-$\frac{1}{1-\frac{1}{m}}$=1-$\frac{m}{m-1}$=-$\frac{1}{m-1}$，a₃=1-$\frac{1}{{a}_{2}}$=1+m-1=m，a₄=1-$\frac{1}{m}$…，
∵2013÷3=671，∴a₂₀₁₃=m，
故答案为：m．

点评此题考查了分式的混合运算，弄清题中的规律是解本题的关键．

练习册系列答案

4.63×10¹⁰

1．

已知：如图，点C是AB的中点，AD=CE，CD=BE．求证：CD∥BE．

18．（2×10³）²×（3×10^-3）=1.2×10⁴．（结果用科学记数法表示）

5．对于锐角α，sinα的值不可能为（　　）

15．

一天早上，马虎同学上学，到校后发现文具盒落在家里，此时离上课开始还有25分钟，于是立即步行回家取文具盒，同时，他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒，两人在途中相遇，相遇后马虎立即坐父亲的自行车赶回学校．如图中线段AB、OB分别表示父子俩在送文具盒过程中，离学校的路程S（米）与所用时间t（分钟）之间的函数关系，结合图象解答下列问题（假设骑自行车和步行的速度始终保持不变）；
（1）求点B的坐标和AB所在直线的函数关系式；
（2）马虎能否在上课前到达学校？

2．先化简，再求值：$\frac{（x-2）（x+3）}{{{x^2}-9}}•\frac{x-3}{{{x^2}-2x}}$，其中x=-2．

19．

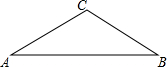如图，已知在等腰△ABC中，∠C=120°
（1）尺规作图：①过点C作CD⊥AC交AB于点D．
②过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；
（2）求证：BC是过A，D，C三点的圆的切线．

20．

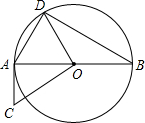如图，AB是⊙O的直径，CA与⊙O相切于点A，点D在⊙O上，且OD⊥OC，
（1）填空：∠ADB=90°°，理由是直径所对的圆周角是直角；
（2）若⊙O的半径为$\sqrt{5}$，AC=2，求BD的长．

试题分类