题目内容
12.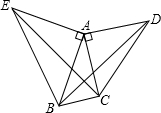 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:(1)旋转中心是A;
(2)逆时针旋转90度;
(3)若EC=10cm,则BD的长度是10cm.
分析 (1)找出两重合三角形的公共顶点即可得出其旋转中心;
(2)根据两重合边所夹的角度即可求出旋转的度数;
(3)根据图形旋转的性质可直接进行解答.
解答 解:(1)∵△EAC逆时针旋转后能与△BAD重合,
∴A点即为两三角形的公共顶点,故旋转中心是A点;
(2)∵△EAC逆时针旋转后能与△BAD,
∴AE与AB重合,
∵∠BAE=90°,
∴旋转的度数为:90;
(3)由题意知EC和BD是对应线段,据旋转的性质可得BD=EC=10cm.
故答案为:(1)A;(2)90;(3)10.
点评 本题考查的是图形旋转的性质,即①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.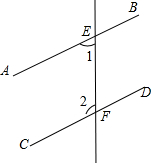 如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠1=55°,则∠2的度数为( )
如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠1=55°,则∠2的度数为( )
 如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠1=55°,则∠2的度数为( )
如图,直线AB∥CD,直线EF分别交AB,CD于点E,F,若∠1=55°,则∠2的度数为( )| A. | 125° | B. | 55° | C. | 35° | D. | 135° |
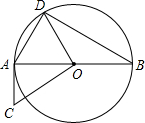 如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
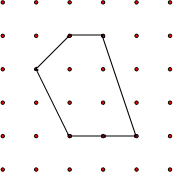 各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6
各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6