题目内容
已知:关于x的方程x2+(2-m)x-2m=0.
(1)求证:无论m取什么实数值,方程总有实数根;
(2)取一个m的值,使得方程两根均为整数,并求出方程的两根.
(1)求证:无论m取什么实数值,方程总有实数根;
(2)取一个m的值,使得方程两根均为整数,并求出方程的两根.
考点:根的判别式
专题:
分析:(1)根据根的判别式的符号进行证明;
(2)在(1)中m的取值范围内取m=0,把m=0代入原方程,求出x的值即可.
(2)在(1)中m的取值范围内取m=0,把m=0代入原方程,求出x的值即可.
解答:解:(1)∵△=(2-m)2-4(-2m)=(2+m)2,
∴无论m取何值,在实数范围内(2+m)2≥0总成立,即△≥0,
∴无论m取什么实数值,方程总有实数根;
(2)取m=0,则原方程化为x2-2x=0,
∴x(x-2)=0,
∴x1=0,x2=2.
∴无论m取何值,在实数范围内(2+m)2≥0总成立,即△≥0,
∴无论m取什么实数值,方程总有实数根;
(2)取m=0,则原方程化为x2-2x=0,
∴x(x-2)=0,
∴x1=0,x2=2.
点评:本题考查的是一元二次方程根的判别式与方程解的关系,解答此题的关键是熟知以下知识,即
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,点A、B、C在圆O上,∠A=60°,则∠BOC的度数是( )
如图,点A、B、C在圆O上,∠A=60°,则∠BOC的度数是( )| A、15° | B、30° |
| C、60° | D、120° |
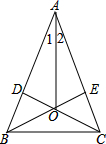 已知:如图,CD⊥AB于D,BE⊥AC于E,CD、BE交于O,∠1=∠2.求证:OB=OC.
已知:如图,CD⊥AB于D,BE⊥AC于E,CD、BE交于O,∠1=∠2.求证:OB=OC. 如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2
如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2