题目内容
如图，已知AB是⊙O的直径，PA切⊙O于点A，OP交⊙O于点C，连接BC，且BC=2| 3 |
考点：切线的性质
专题：
分析：连结AC，根据切线的性质得AB⊥PA，即∠OAP=90°，由于∠P=30°，则∠AOP=60°，根据三角形外角性质易得∠B=30°，由AB为直径，根据圆周角定理得∠ACB=90°，然后利用∠B的余弦即可得到直径AB=4，则⊙O的半径为2．
解答：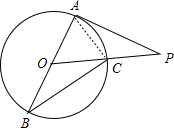
解：连结AC，如图，
∵PA切⊙O于点A，
∴AB⊥PA，
∴∠OAP=90°，
∵∠P=30°，
∴∠AOP=60°，
∵OB=OC，
∴∠B=∠OCB，
∴∠AOC=2∠B，
∴∠B=30°，
∵AB为直径，
∴∠ACB=90°，
∴cosB=
∴AB=
=4，
∴OA=2，
即⊙O的半径为2．
解：连结AC，如图，∵PA切⊙O于点A，
∴AB⊥PA，
∴∠OAP=90°，
∵∠P=30°，
∴∠AOP=60°，
∵OB=OC，
∴∠B=∠OCB，
∴∠AOC=2∠B，
∴∠B=30°，
∵AB为直径，
∴∠ACB=90°，
∴cosB=
| BC |
| AB |
∴AB=
2
| ||||
|
∴OA=2，
即⊙O的半径为2．
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．
练习册系列答案
相关题目
如图，有一块直角三角形纸片沿直线AD折叠，使AC落在斜边AB上，且点C与点E重合．已知两直角边AC=6cm，BC=8cm，求CD的长．
如图，点B在线段AC上，点E在线段BD上，∠ABD=∠DBC，AB=DB，EB=CB，M、N分别是AE、CD的中点，判断BM与BN的关系，并说明理由．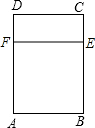
现有铝合金窗框材料8米，准备用它做一个如图所示的长方形窗架（窗架宽度AB必须小于窗架的高度BC）．已知窗台距离房屋天花板2.2米．设AB为x米，窗架的总面积为S平方米．试写出S与x的函数关系式，并求自变量x的取值范围．