题目内容
小明认为教科书介绍的转盘游戏不易操作,于是他用20个除颜色外都相同的小球,进行摸球游戏,这20个球中有1个红球,2个黄球,4个绿球,13个白球,每次从中摸出1球,并规定:摸到红球可获得100元购物券,摸到黄球可获得50元购物券,摸到绿球可获得20元购物券,摸到白球则不能获购物券,求每次摸球所获购物券的平均数,并与课本的转盘实验中的结果相比较,说明其中的原因.
考点:模拟实验
专题:
分析:首先利用概率公式求出摸到个小球的概率,进而求出每次摸球所获购物券的平均数,进而比较得出答案.
解答:解:∵20个球中有1个红球,2个黄球,4个绿球,13个白球,每次从中摸出1球,
摸到红球可获得100元购物券,摸到黄球可获得50元购物券,摸到绿球可获得20元购物券,摸到白球则不能获购物券,
∴摸到红球的概率为:
,摸到黄球的概率为:
=
,摸到绿球的概率为:
=
∴每次摸球所获购物券的平均数为:100×
+50×
+20×
=14(元),
与课本中的转盘游戏的结果一致,原因是所获购物卷的平均数值与每种面额购物券出现的概率有关.
摸到红球可获得100元购物券,摸到黄球可获得50元购物券,摸到绿球可获得20元购物券,摸到白球则不能获购物券,
∴摸到红球的概率为:
| 1 |
| 20 |
| 2 |
| 20 |
| 1 |
| 10 |
| 4 |
| 20 |
| 1 |
| 5 |
∴每次摸球所获购物券的平均数为:100×
| 1 |
| 20 |
| 1 |
| 10 |
| 1 |
| 5 |
与课本中的转盘游戏的结果一致,原因是所获购物卷的平均数值与每种面额购物券出现的概率有关.
点评:此题主要考查了模拟实验以及概率公式的应用,得出每次摸球所获购物券的平均数是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各组数作为三角形的边长,其中不能构成直角三角形的是( )
| A、6,8,10 |
| B、5,12,13 |
| C、9,40,41 |
| D、7,9,12 |
 如图,已知△ABC≌△ABD,∠1=35°,∠D=40°,则∠CBE=
如图,已知△ABC≌△ABD,∠1=35°,∠D=40°,则∠CBE=
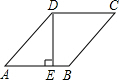 如图,在菱形ABCD中,DE⊥AB于E,DE=8,sinA=
如图,在菱形ABCD中,DE⊥AB于E,DE=8,sinA= 如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.