题目内容
已知a，b为有理数且满足a2+b2+5=4a-2b，则（a+b）2013= ．
考点：因式分解-运用公式法,非负数的性质：偶次方
专题：
分析：首先利用完全平方公式得出a，b的值，进而得出答案．
解答：解：∵a2+b2+5=4a-2b，
∴（a-2）2+（b+1）2=0，
∴a=2，b=-1，
∴（a+b）2013=1．
故答案为：1．
∴（a-2）2+（b+1）2=0，
∴a=2，b=-1，
∴（a+b）2013=1．
故答案为：1．
点评：此题主要考查了完全平方公式的应用，正确得出a，b的值是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
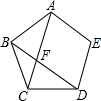如图所示，正五边形ABCDE，连接对角线AC、BD，设AC与BD相交于点F．已知x=
+1，且x2=ax+b，则a，b的值分别为（ ）
| 5 |
| A、1，2 | B、2，2 |
| C、2，3 | D、2，4 |
如图，壁虎在一个圆柱形油罐的下底边沿A处，它发现在B处有一只苍蝇，壁虎决定尽快捉到这只苍蝇，获得一顿美餐，请问壁虎从A处到B处的最短路线是什么？