题目内容
8.观察:a1=1-$\frac{1}{m}$,a2=1-$\frac{1}{{a}_{1}}$,a3=1-$\frac{1}{{a}_{2}}$,a4=1-$\frac{1}{{a}_{3}}$,…,则a2015=-$\frac{1}{m-1}$(用含m的代数式表示).分析 先计算得到a1=$\frac{m-1}{m}$a2=1-$\frac{1}{{a}_{1}}$=$\frac{-1}{m-1}$,a3=1-$\frac{1}{{a}_{2}}$=m,a4=1-$\frac{1}{m}$,由此可得a2015=-$\frac{1}{m-1}$.
解答 解:a1=1-$\frac{1}{m}$=$\frac{m-1}{m}$
a2=1-$\frac{1}{{a}_{1}}$=1-$\frac{m}{m-1}$=$\frac{-1}{m-1}$
a3=1-$\frac{1}{{a}_{2}}$=m,
a4=1-$\frac{1}{{a}_{3}}$=1-$\frac{1}{m}$
而2015=3×671+1,
所以a2015=a2=-$\frac{1}{m-1}$.
故答案为-$\frac{1}{m-1}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.也考查了实数的运算.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
18. 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
 现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
现有7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=2b | B. | a=3b | C. | a=3.5b | D. | a=4b |
3.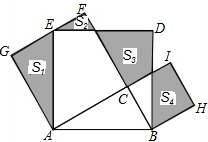 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )
 如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=12,BC=5,分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH,四块阴影部分的面积分别为S1、S2、S3、S4,则S1+S2+S3+S4等于( )| A. | 60 | B. | 90 | C. | 144 | D. | 169 |
13.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (-x+y)(-x-y) | C. | (x+y)(-x+y) | D. | (x-y)(-x+y) |
17.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (x+y)(x-y) | C. | (x+y)(-x-y) | D. | (-x-y)(-x+y) |
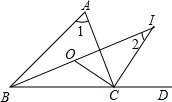 △ABC中,∠ABC=40°,∠ACB=80°,BO、CO分别平分∠ABC,∠ACB,交于O,CI为外角∠ACD的平分线,BO的延长线交CI于I点,记∠BAC=∠1,∠BIC=∠2,则∠1:∠2=2:1(求比值).
△ABC中,∠ABC=40°,∠ACB=80°,BO、CO分别平分∠ABC,∠ACB,交于O,CI为外角∠ACD的平分线,BO的延长线交CI于I点,记∠BAC=∠1,∠BIC=∠2,则∠1:∠2=2:1(求比值).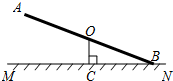 如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm.
如图,O为跷跷板AB的中点,支柱OC与地面MN垂直,垂足为点C,且OC=50cm,当跷跷板的一端B着地时,另一端A离地面的高度为100cm.