题目内容
4.解方程:(1)(x-2)(x-3)=12
(2)3y2+1=2$\sqrt{3}$y.
分析 (1)首先把方程整理成一元二次方程的一般式,然后利用因式分解法解方程即可;
(2)首先把方程整理成一元二次方程的一般式,然后利用求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$进行计算即可.
解答 解:(1)(x-2)(x-3)=12,
整理得:x2-5x-6=0,
(x-6)(x+1)=0,
则x-6=0,x+1=0,
解得:x1=-1;x2=6;
(2)3y2-2$\sqrt{3}$y+1=0,
∵a=3,b=-2$\sqrt{3}$,c=1,
∴△=b2-4ac=12-12=0,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{2\sqrt{3}±0}{6}$=$\frac{\sqrt{3}}{3}$,
∴y1=y2=$\frac{{\sqrt{3}}}{3}$.
点评 此题主要考查了一元二次方程的解法,关键是掌握因式分解法和公式法解方程的步骤.

练习册系列答案
相关题目
19.在△ABC和△A'B'C'中,AB=A'B',∠B=∠B',补充条件后仍不一定能保证△ABC≌△A'B'C',则补充的这个条件是( )
| A. | BC=B'C' | B. | ∠A=∠A' | C. | AC=A'C' | D. | ∠C=∠C' |
 如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是10.
如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是10.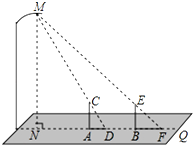 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米)
晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小军正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小聪正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高BE为1.74米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高AC的长(结果精确到0.01米) 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、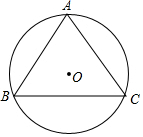 求正三角形的内切圆半径、外接圆半径和高的比.
求正三角形的内切圆半径、外接圆半径和高的比.