题目内容
3.阳光百货超市直接从厂家购进A、B两种酱油,A种酱油每瓶进价6.5元,B种酱油每瓶进价8元,该超市购进A、B两种酱油共200瓶,总进价不超过1420元.(1)该超市至少购进A种酱油多少瓶?
(2)若该超市将A、B两种酱油的售价分别定为每瓶8元和10元,且将这200瓶酱油卖完获利不低于339元,请你写出所有的进货方案.
分析 (1)求A,B两种酱油各购进多少瓶,根据题意购进200瓶,总进价不超过1420元,可列不等式求解.
(2)由题意可列不等式组,解得120≤a≤122.因为a为非负整数,所以a取120,121,122.所以200-a=80或79或78.
解答 解:(1)设:该百货超市购进A种酱油x瓶,B种酱油(200-x)瓶,
由题意可得:6.5x+8(200-x)≤1420,
解得:x≥12.
答:该百货超市购进A种酱油至少12瓶;
(2)设购进A种酱油a瓶,B种酱油(200-a)瓶,
由题意可知6.5a+8(200-a)≤1420,
1.5a+2(200-a)≥339,
解得120≤a≤122.因为a为非负整数,所以a取120,121,122.所以200-a=80或79或78.
答:该百货超市有三种购货方案:A种酱油进120瓶,B种酱油进80瓶;
A种酱油进121瓶,B种酱油进79瓶;
A种酱油进122瓶,B种酱油进78瓶.
点评 本题综合考查了一元一次不等式在实际生活中的应用.解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.要会用分类的思想来讨论问题并能用不等式的特殊值来求得方案的问题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.
如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.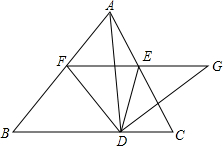 如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.
如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.