题目内容
6.先化简,再求值:($\frac{{a}^{2}-5a+2}{a+2}$+1)÷$\frac{{a}^{2}-4}{{a}^{2}+4a+4}$,其中a=$\frac{3}{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=$\frac{{a}^{2}-5a+2+a+2}{a+2}$•$\frac{(a+2)^{2}}{(a+2)(a-2)}$
=$\frac{{a}^{2}-4a+4}{a+2}$•$\frac{{(a+2)}^{2}}{(a+2)(a-2)}$
=$\frac{{(a-2)}^{2}}{a+2}$•$\frac{{(a+2)}^{2}}{(a+2)(a-2)}$
=a-2,
当a=$\frac{3}{2}$时,原式=$\frac{3}{2}$-2=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
14.如果反比例函数y=$\frac{m+1}{x}$在每个分支上函数值y随自变量x的增大而减小,那么m的取值范围是( )
| A. | m>-1 | B. | m≥-1 | C. | m<-1 | D. | m≤-1 |
11.吉林省春节黄金周期间,共接待游客8 897 700,这个数字用科学记数法表示为( )
| A. | 88.977×105 | B. | 8.8977×106 | C. | 0.88977×103 | D. | 8.897×103 |
16. 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )
 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 正三棱柱 | D. | 正三棱锥 |
 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C. 一大门的栏杆如图所示,BA⊥AE,若CD∥AE,则∠ABC+∠BCD=270度.
一大门的栏杆如图所示,BA⊥AE,若CD∥AE,则∠ABC+∠BCD=270度.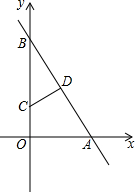 如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.
如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A(6,0)、点B(0,6$\sqrt{3}$),点D是线段AB的中点,点C(0,2$\sqrt{3}$),点E为x轴上一动点.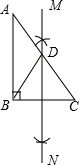 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:
如图,在Rt△ABC中,∠B=90°,按如下步骤作图: 如图,圆O的半径为3,点A、B、C在圆O上,且∠ACB=45°,则弦AB的长是3$\sqrt{2}$.
如图,圆O的半径为3,点A、B、C在圆O上,且∠ACB=45°,则弦AB的长是3$\sqrt{2}$.