题目内容
已知⊙M与⊙N的半径分别为1和5,若两圆相切,那么这两圆的圆心距MN的长等于( )
| A、4 | B、6 | C、4或5 | D、4或6 |
考点:圆与圆的位置关系
专题:
分析:外切时,圆心距为1+5=6;内切时,圆心距5-1=4.
解答:解:∵两圆相切,
∴两圆可能外切和内切,
∴外切时,圆心距为1+5=6;
内切时,圆心距为5-1=4.
∴圆心距为6或4.
故选D.
∴两圆可能外切和内切,
∴外切时,圆心距为1+5=6;
内切时,圆心距为5-1=4.
∴圆心距为6或4.
故选D.
点评:考查了圆与圆的位置关系,本题用到的知识点为:两圆外切,圆心距=两圆半径之和.两圆内切,圆心距=两圆半径之差.

练习册系列答案
相关题目
在直角坐标系中,点M(1,-2012)关于原点的对称点坐标是( )
| A、(1,2012) |
| B、(-1,-2012) |
| C、(-1,2012) |
| D、(-2012,1) |
在Rt△ABC中,已知∠ACB=90°,BC=1,AB=2,那么下列结论正确的是( )
A、sinA=
| ||||
B、tanA=
| ||||
C、cosB=
| ||||
D、cotB=
|
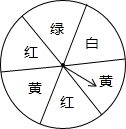 如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题:
如图,有一个转盘被分成6个相同的扇形区域,颜色分别为红、黄、绿、白四中颜色,指针的位置固定,转动转盘后任其自由停止,如果指针指在等分线上,那么重新转动,直至指针指向某个扇形区域内为止,请你完成以下问题: 如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为
如图,水库大坝的横截面是梯形,坝顶AD宽5米,坝高10米,斜坡CD的坡角为45°,斜坡AB的坡度i=1:1.5,那么坝底BC的长度为 一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是
一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是 我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足:
我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足: