题目内容
1. 我国的“蛟龙号”创造了世界同类潜水器最大下潜深度纪录7062米.如图,
我国的“蛟龙号”创造了世界同类潜水器最大下潜深度纪录7062米.如图,在某次任务中,“蛟龙号”在点A处测得正前方海底沉船C的俯角为45°,然后在同一深度向正前方直线航行600米到点B,此时测得海底沉船C的俯角为60°,那么“蛟龙号”在点B下潜到沉船C处,下潜的垂直深度是( )米.
| A. | 600-600$\sqrt{3}$ | B. | 600+600$\sqrt{3}$ | C. | 900-300$\sqrt{3}$ | D. | 900+300$\sqrt{3}$ |
分析 作CD⊥AB于点D,在直角△ACD和直角△BCD中分别利用三角函数表示出AD和BD的长,然后根据AB=AD-BD即可列方程求解.
解答  解:作CD⊥AB于点D.
解:作CD⊥AB于点D.
设CD=x(米),
∵在直角△ACD中,tan∠CAD=$\frac{CD}{AD}$,即$\frac{x}{AD}$=tan45°=1,
∴AD=CD=x(米).
同理,BD=$\frac{CD}{tan∠CBD}$=$\frac{x}{tan50°}$=$\frac{\sqrt{3}x}{3}$(米).
∵AB=AD-BD,
∴x-$\frac{\sqrt{3}}{3}$x=600,
解得:x=900+300$\sqrt{3}$.
故选D.
点评 本题考查俯角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{30}$ | B. | $\sqrt{18}$ | C. | $\sqrt{9}$ | D. | $\sqrt{\frac{1}{3}}$ |
 如图,在直角坐标系中,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,在直角坐标系中,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?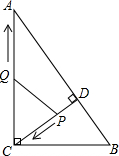 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.