题目内容
14.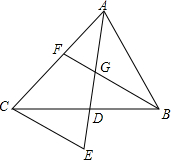 如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.
如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.
分析 根据ASA证明△DBG与△DCE全等,再利用三角形中线的性质解答即可.
解答 解:∵CE∥FB,
∴∠GBD=∠ECD,
∵AD,BF为中线,
∴CD=DB,
在△DBG与△DCE中,
$\left\{\begin{array}{l}{∠GBD=∠ECD}\\{CD=DB}\\{∠CDE=∠BDG}\end{array}\right.$,
∴△DBG≌△DCE,
∴DG=DE,
∵AG=6cm,
∴DE=3cm.
点评 本题考查了全等三角形的判定和性质,正确证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.用给定长度的绳子围成下面四种几何图形,其面积一定最大的是( )
| A. | 三角形 | B. | 平行四边形 | C. | 正方形 | D. | 菱形 |
4.下列运算正确的是( )
| A. | a3÷a=a3(a≠0) | B. | (-a)4=a4 | C. | 3a2•2a2=6a2 | D. | (a-b)2=a2-b2 |
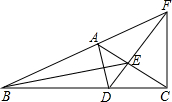 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.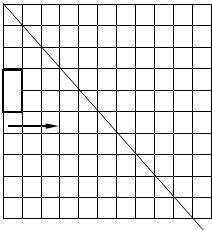 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线