题目内容
19.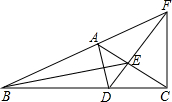 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
分析 过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,推出△AFN≌△AFR,根据全等三角形的性质得到FN=FR,由CF为△ABC的外角平分线,得到FR=FT,证得DF平分∠ADC,然后根据角平分线的性质即可得到结论.
解答 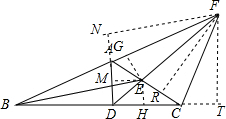 解:过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,
解:过F作FN⊥AD于N,FR⊥AC于R,FT⊥BC于T,过E作EM⊥AD于M,EH⊥BC于H,EG⊥AB于G,
∵∠BAC=120°,AD为△ABC的内角平分线,
∴∠FAN=∠BAD=60°,∠RAF=60°,
在△AFN与△AFR中,
$\left\{\begin{array}{l}{∠N=∠FRA=90°}\\{∠FAN=∠FAG=60°}\\{AF=AF}\end{array}\right.$,
∴△AFN≌△AFR,
∴FN=FR,
∵CF为△ABC的外角平分线,
∴FR=FT,
∴NF=FT,
∴DF平分∠ADC,
∴ME=EH,
∵∠DAC=∠CAF=60°,
∴EG=EM,
∴EG=EH,
∴BE平分∠ABC.
点评 本题考查了全等三角形的判定和性质,角平分线的定义和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
9.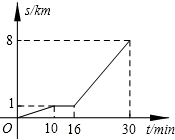 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )| A. | 他离家8千米,共用了30分钟 | B. | 他等公交车时间为6分钟 | ||
| C. | 他步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
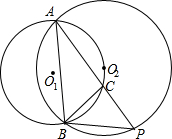 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)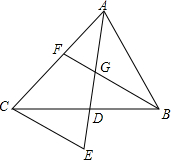 如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.
如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.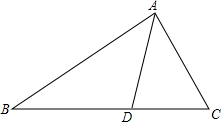 △ABC中,D是BC上的点,AD平分∠BAC,BD=2DC,若∠BAC=60°,求∠B.
△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC,若∠BAC=60°,求∠B.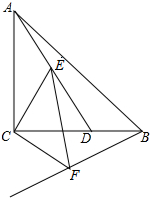 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF. 如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.
如图,在△ABC中,D是BC上一点,且AB=BD=3CD,若cos∠DAC=$\frac{7}{8}$,AD=6,则AC=8.