题目内容
2.已知抛物线y=mx2+2mx+n交x轴于A、B两点,交y轴于C(0,3),顶点为D,且AB=4.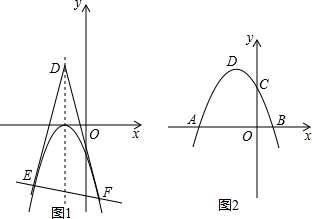
(1)求抛物线的解析式;
(2)点P为对称轴右侧抛物线上一点,点S在x轴上,当△DPS为等腰直角三角形时,求点P的坐标;
(3)将抛物线沿对称轴向下平移,使顶点落在x轴上,设点D关于x轴的对称点为M,过M的直线交抛物线于E、F(点E在对称轴左侧),连DE,DF,且S△DEF=20.求E、F的坐标.
分析 (1)可根据抛物线的对称性求出点A、B的坐标,然后用待定系数法就可解决问题;
(2)由于等腰直角△DPS的直角顶点不确定,可分三种情况讨论,然后只需通过构造K型相似,用一个字母表示点P的坐标,代入抛物线的解析式就可解决问题;
(3)过点E作EG⊥DM于G,过点F作FH⊥DM于H,如图2.设E(x1,y1),F(x2,y2),由S△DEF=20可得到x2-x1=5,易得EF的解析式y=kx+k-4,代入y=-x2-2x-1,只需运用根与系数的关系就可解决问题.
解答 解:(1)抛物线y=mx2+2mx+n的对称轴为x=-$\frac{2m}{2m}$=-1.
由AB=4,根据抛物线的对称性可得:
A(-1-$\frac{4}{2}$,0)即(-3,0),B(-1+$\frac{4}{2}$,0)即(1,0).
将点B、C的坐标代入y=mx2+2mx+n,得
$\left\{\begin{array}{l}{m+2m+n=0}\\{n=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\\{\;}\end{array}\right.$,
∴抛物线的解析式为y=-x2-2x+3;
(2)由y=-x2-2x+3可得顶点D的坐标为(-1,4),设P(p,q).
①当∠DPS=90°,PD=PS时,
过点P作PN⊥x轴于N,过点D作DM⊥PN于M,如图1①.
则有∠DMP=∠PNS=90°,∠MDP=∠NPS=90°-∠MPD.
在△DMP和△PNS中,
$\left\{\begin{array}{l}{∠DMP=∠PNS}\\{∠MDP=∠NPS}\\{PD=PS}\end{array}\right.$,
∴△DMP≌△PNS,
∴DM=PN=q,
∴点P的坐标为(-1+q,q),
∴q=-(-1+q)2-2(-1+q)+3,
整理得q2+q-4=0,
解得q1=$\frac{-1+\sqrt{17}}{2}$,q2=$\frac{-1-\sqrt{17}}{2}$,
∵点P为对称轴右侧抛物线上一点,
∴-1+q>-1即q>0,
∴点P的坐标为($\frac{\sqrt{17}-3}{2}$,$\frac{-1+\sqrt{17}}{2}$);
②当∠SDP=90°,DS=DP时,
过点P、S作x轴的垂线,与过点D垂直于y轴的直线分别交于点M、N,如图1②.
同理可得:点P的坐标为(3,-12);
③当∠DSP=90°,SD=SP时,
过点D、P作y轴的垂线,与过点S垂直于x轴的直线分别交于点M、N,如图1③.
同理可得:点P的坐标为($\frac{-3+\sqrt{33}}{2}$,$\frac{-9+\sqrt{33}}{2}$).
综上所述:当△DPS为等腰直角三角形时,
点P的坐标为($\frac{\sqrt{17}-3}{2}$,$\frac{-1+\sqrt{17}}{2}$),(3,-12),($\frac{-3+\sqrt{33}}{2}$,$\frac{-9+\sqrt{33}}{2}$);
(3)过点E作EG⊥DM于G,过点F作FH⊥DM于H,如图2.
设E(x1,y1),F(x2,y2),则
EG=-1-x1,FH=x2-(-1)=x2+1.
∵点D与点M关于x轴对称,
∴M(-1,-4),DM=4-(-4)=8.
∵S△DEF=20,
∴$\frac{1}{2}$×8×(-1-x1)+$\frac{1}{2}$×8×(x2+1)=4(x2-x1)=20,
∴x2-x1=5.
设过点M的直线的解析式为y=kx+b,
∴-4=-k+b,
∴b=k-4,
∴过点M的直线的解析式为y=kx+k-4.
由题可知:平移后的抛物线的解析式为y=-(x+1)2.
将y=kx+k-4代入y=-x2-2x-1中,得
x2+(k+2)x+k-3=0,
∴x1+x2=-(k+2),x1•x2=k-3,
∴(x1-x2)2=(x1+x2)2-4x1•x2=(k+2)2-4(k-3)=25,
解得k=±3.
①当k=-3时,直线EF的解析式为y=-3x-7,
解方程组$\left\{\begin{array}{l}{y=-3x-7}\\{y=-(x+1)^{2}}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-16}\end{array}\right.$,
∴E(-2,-1),F(3,-16);
②当k=3时,直线EF的解析式为y=3x-1,
解方程组$\left\{\begin{array}{l}{y=3x-1}\\{y=-(x+1)^{2}}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-5}\\{y=-16}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$,
∴E(-5,-16),F(0,-1).
点评 本题主要考查了运用待定系数法求二次函数的解析式、抛物线的轴对称性、根与系数的关系、相似三角形的判定与性质、解一元二次方程、解方程组等知识,运用分类讨论并构造K型相似是解决第(2)小题的关键,运用根与系数的关系是解决第(3)小题的关键.

| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
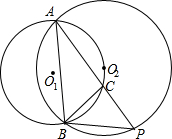 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)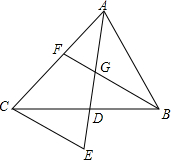 如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.
如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.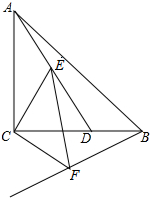 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF. 如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).
如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).