题目内容

6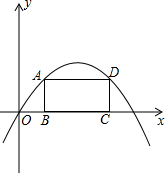．如图，抛物线的解析式为y=-x2+6x，矩形边BC在x轴上，A，D在抛物线上（第一象限内）．求矩形周长的最大值．

分析 设B（x，0），则由对称性可分别表示出C、A、D的坐标，分别表示出矩形的长和宽，再进一步根据矩形的周长公式进行计算，最后根据二次函数的最值方法进行求解．

解答 解：设B（x，0），则由对称性得C（6-x，0），A（x，-x2+6x），D（6-x，-x2+6x），
故可得l=2（AB+BC）=2[（6-2x）+（-x2+6x）]=-2（x-2）2+20，
则当x=2时，l有最大值，最大值为20．

点评 本题主要考查了二次函数的性质及最值，要求我们能够利用建立函数关系式的方法求得周长的最值，难度适中．

练习册系列答案
相关题目
16．因式分解：x2-4xy-2x+4y2+4y-3=（x-2y-3）（x-2y+1）．
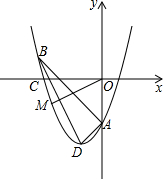17．在某节习题课上，老师在黑板上写下了关于x的二次函数y=kx2+（k+1）x+2-4k．
（1）某两位同学经过思考，对上述的二次函数进行了如下总结：
①该二次函数的图象经过点（1，3）；
②当k＜0时，该二次函数的图象与y轴的正半轴有交点；
请你判断上面两条结论是真命题还是假命题，并说明理由；
（2）若二次函数y=kx2+（k+1）x+2-4k的图象如图所示，该函数图象经过点B（-3，1）且与y轴交于点A，与x轴的负半轴交于点C，D为图象的顶点．
①求∠BAD的度数；
②点M在第三象限，且点M在二次函数图象上，连接OM．若∠ABD=∠MOC，求点M的横坐标．
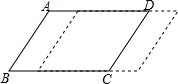14．如图所示，平行四边形ABCD底边BC上的高为6cm，当边DC向右平移时，平行四边形的面积发生了变化．
（1）这个变化过程中，自变量、因变量各是什么？
（2）如果底边BC的长为xcm，那么平行四边形的面积y（cm2）可以表示为y=5x；
（3）当底边BC的长从12cm增加到20cm时，平行四边形ABCD的面积增加了多少？
1．若（mx4）•（4xk）=12x12，则m=3，k=8．
11．下列一元二次方程中，没有实数根的是（　　）
A．x2-3x-l=0B．x2-1=0C．x2-2x+l=0D．x2+2x+3=0
18．计算：（x+2）（x-2）-（x-1）2=2x-5．
15．已知：4x-3y-6z=0，x+2y-7z=0（xyz≠0），则$\frac{2x+3y+6z}{x+4y+7z}$=1．
16．已知关于x的一元二次方程3x2+mx-2=0的一个解与方程$\frac{5}{x-3}$=$\frac{2}{x}$的解相同．
（1）解方程：$\frac{5}{x-3}$=$\frac{2}{x}$；
（2）求m的值，并求出方程3x2+mx-2=0的另一个解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网