题目内容
14.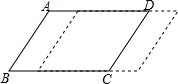 如图所示,平行四边形ABCD底边BC上的高为6cm,当边DC向右平移时,平行四边形的面积发生了变化.
如图所示,平行四边形ABCD底边BC上的高为6cm,当边DC向右平移时,平行四边形的面积发生了变化.(1)这个变化过程中,自变量、因变量各是什么?
(2)如果底边BC的长为xcm,那么平行四边形的面积y(cm2)可以表示为y=5x;
(3)当底边BC的长从12cm增加到20cm时,平行四边形ABCD的面积增加了多少?
分析 (1)根据自变量和因变量的定义即可确定;
(2)根据平行四边形的面积公式求解;
(3)根据(2)的结果即可直接求解.
解答 解:(1)自变量是边BC的长,因变量是平行四边形的面积;
(2)平行四边形的面积y(cm2)可以表示为:y=5x;
(3)平行四边形ABCD的面积增加的数值是:5(20-12)=40(cm2).
点评 本题考查了常量与变量的定义以及平行四边形的面积公式,函数的关系式,是一个基础题.

练习册系列答案
相关题目
2. 如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
 如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )| A. | (-1,1) | B. | (-2,-1) | C. | (-3,1) | D. | (1,-2) |
9.下列计算中正确的是( )
| A. | a2+b3=2a5 | B. | a4÷a=a4 | C. | a2•a4=a8 | D. | (a2)3=a6 |
3.计算(0.04)2013×[(-5)2012]2的正确结果是( )
| A. | 0.04 | B. | -5 | C. | 3 | D. | 4 |
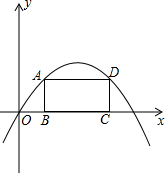 如图,抛物线的解析式为y=-x2+6x,矩形边BC在x轴上,A,D在抛物线上(第一象限内).求矩形周长的最大值.
如图,抛物线的解析式为y=-x2+6x,矩形边BC在x轴上,A,D在抛物线上(第一象限内).求矩形周长的最大值.