题目内容
如图,已知在梯形ABCD中,AD∥BC,AB⊥BC,AB=4,AD=3,sin∠DCB=
,P是边CD上一点(点P与点C、D不重合),以PC为半径的⊙P与边BC相交于点C和点Q.

(1)如果BP⊥CD,求CP的长;
(2)如果PA=PB,试判断以AB为直径的⊙O与⊙P的位置关系;
(3)联结PQ,如果△ADP和△BQP相似,求CP的长.
| 4 |
| 5 |

(1)如果BP⊥CD,求CP的长;
(2)如果PA=PB,试判断以AB为直径的⊙O与⊙P的位置关系;
(3)联结PQ,如果△ADP和△BQP相似,求CP的长.
考点:圆的综合题
专题:综合题
分析:(1)作DH⊥BC于H,如图1,利用矩形的性质得DH=4,BH=3,在Rt△DHC中,利用正弦的定义可计算出DC=5,再利用勾股定理计算出CH=3,则BC=BH+CH=6,然后证明Rt△DCH∽Rt△BCP,利用相似比可计算出PC=
;
(2)作PE⊥AB于E,如图2,由于PA=PB,根据等腰三角形的性质得AE=BE=
AB=2,也可判断PE为梯形ABCD的中位线,所以PD=PC=
,PE=
(AD+BC)=
,于是得到EA+PC=PE,根据两圆外切的判定方法得到以AB为直径的⊙O与⊙P外切;
(3)如图1,作PF⊥BC于F,根据垂径定理得CF=QF,设PC=x,则DP=5-x,先证明△CPF∽△CDH,利用相似比可计算出CF=
,则CQ=2CF=
,BQ=BC-CQ=6-
,由PQ=PC得∠PQC=∠PCQ,而∠ADP+∠PCQ=180°,∠PQC+∠PQB=180°,所以∠ADP=∠PQB,然后讨论:当△ADP∽△BQP,根据相似的性质得
,解得x1=
,x2=10(舍去),得到PC=
;当△ADP∽△PQB,利用相似的性质得
=
,解得x1=
,x2=5(舍去),得到PC=
.
| 18 |
| 5 |
(2)作PE⊥AB于E,如图2,由于PA=PB,根据等腰三角形的性质得AE=BE=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
(3)如图1,作PF⊥BC于F,根据垂径定理得CF=QF,设PC=x,则DP=5-x,先证明△CPF∽△CDH,利用相似比可计算出CF=
| 3x |
| 5 |
| 6x |
| 5 |
| 6x |
| 5 |
| 3 | ||
6-
|
| 5-x |
| x |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| x |
| 5-x | ||
6-
|
| 18 |
| 5 |
| 18 |
| 5 |
解答:解:(1)作DH⊥BC于H,如图1,
∵AD∥BC,AB⊥BC,AB=4,AD=3,
∴DH=4,BH=3,
在Rt△DHC中,sin∠DCH=
=
,
∴DC=5,
∴CH=
=3,
∴BC=BH+CH=6,
∵BP⊥CD,
∴∠BPC=90°,
而∠DCH=∠BCP,
∴Rt△DCH∽Rt△BCP,
∴
=
,即
=
,
∴PC=
;
(2)作PE⊥AB于E,如图2,
∵PA=PB,
∴AE=BE=
AB=2,
∵PE∥AD∥BC,
∴PE为梯形ABCD的中位线,
∴PD=PC,PE=
(AD+BC)=
(3+6)=
,
∴PC=
DC=
,
∴EA+PC=PE,
∴以AB为直径的⊙O与⊙P外切;
(3)如图1,作PF⊥BC于F,则CF=QF,
设PC=x,则DP=5-x,
∵PF∥DH,
∴△CPF∽△CDH,
∴
=
,即
=
,解得CF=
,
∴CQ=2CF=
,
∴BQ=BC-CQ=6-
,
∵PQ=PC,
∴∠PQC=∠PCQ,
∵AD∥BC,
∴∠ADP+∠PCQ=180°,
而∠PQC+∠PQB=180°,
∴∠ADP=∠PQB,
当△ADP∽△BQP,
∴
=
,即
=
,
整理得2x2-25x+50=0,解得x1=
,x2=10(舍去),
经检验x=
是原分式方程的解.
∴PC=
;
当△ADP∽△PQB,
∴
=
,即
=
整理得5x2-43x+90=0,解得x1=
,x2=5(舍去),
经检验x=
是原分式方程的解.
∴PC=
,
∴如果△ADP和△BQP相似,CP的长为
或
.
∵AD∥BC,AB⊥BC,AB=4,AD=3,
∴DH=4,BH=3,
在Rt△DHC中,sin∠DCH=
| DH |
| DC |
| 4 |
| 5 |
∴DC=5,
∴CH=
| DC2-DH2 |
∴BC=BH+CH=6,
∵BP⊥CD,
∴∠BPC=90°,
而∠DCH=∠BCP,
∴Rt△DCH∽Rt△BCP,
∴
| DC |
| BC |
| CH |
| PC |
| 5 |
| 6 |
| 3 |
| PC |
∴PC=
| 18 |
| 5 |

(2)作PE⊥AB于E,如图2,
∵PA=PB,
∴AE=BE=
| 1 |
| 2 |
∵PE∥AD∥BC,
∴PE为梯形ABCD的中位线,
∴PD=PC,PE=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴PC=
| 1 |
| 2 |
| 5 |
| 2 |
∴EA+PC=PE,
∴以AB为直径的⊙O与⊙P外切;
(3)如图1,作PF⊥BC于F,则CF=QF,
设PC=x,则DP=5-x,
∵PF∥DH,
∴△CPF∽△CDH,
∴
| PC |
| CD |
| CF |
| CH |
| x |
| 5 |
| CF |
| 3 |
| 3x |
| 5 |
∴CQ=2CF=
| 6x |
| 5 |
∴BQ=BC-CQ=6-
| 6x |
| 5 |
∵PQ=PC,
∴∠PQC=∠PCQ,
∵AD∥BC,
∴∠ADP+∠PCQ=180°,
而∠PQC+∠PQB=180°,
∴∠ADP=∠PQB,
当△ADP∽△BQP,
∴
| AD |
| BQ |
| DP |
| QP |
| 3 | ||
6-
|
| 5-x |
| x |
整理得2x2-25x+50=0,解得x1=
| 5 |
| 2 |
经检验x=
| 5 |
| 2 |
∴PC=
| 5 |
| 2 |
当△ADP∽△PQB,
∴
| AD |
| PQ |
| DP |
| BQ |
| 3 |
| x |
| 5-x | ||
6-
|
整理得5x2-43x+90=0,解得x1=
| 18 |
| 5 |
经检验x=
| 18 |
| 5 |
∴PC=
| 18 |
| 5 |
∴如果△ADP和△BQP相似,CP的长为
| 5 |
| 2 |
| 18 |
| 5 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆与圆的位置关系和梯形的性质;会运用勾股定理和相似比进行几何计算.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.
已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.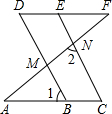 如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程:
如图,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程: