题目内容
18.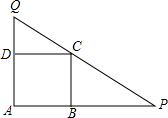 如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
如图,已知正方形ABCD的边长为1,过顶点C的直线与射线AB、AD分别交于点P,Q.求$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值.
分析 根据已知条件推出△QDC∽△QAP,△PBC∽△PAQ,根据相似三角形的性质得到$\frac{AD}{AQ}=\frac{CD}{PQ}$,$\frac{AB}{AP}=\frac{CQ}{PQ}$,于是得到$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$=1+$\frac{1}{PQ}$,推出要使$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$最大,则PQ最小即可,于是得到当AP=AQ时,PQ最小,根据勾股定理得到PQ=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,即可得到结论.
解答 解:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∴△QDC∽△QAP,△PBC∽△PAQ,
∴$\frac{AD}{AQ}=\frac{CD}{PQ}$,$\frac{AB}{AP}=\frac{CQ}{PQ}$,
即$\frac{1}{AQ}=\frac{CP}{PQ}$,$\frac{1}{AP}=\frac{CQ}{PQ}$,
∴$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$=1+$\frac{1}{PQ}$,
∴要使$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$最大,则PQ最小即可,
∴当AP=AQ时,PQ最小,
此时∠P=45°=∠BCP,
∴BC=BP=1,同理DQ=1,
∴PQ=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的最大值=1+$\frac{1}{2\sqrt{2}}$=1+$\frac{\sqrt{2}}{4}$.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,正方形的性质,知道当AP=AQ时,$\frac{1}{AP}+\frac{1}{AQ}+\frac{1}{PQ}$的值最大是解题的关键.

| A. | x>6 | B. | x≥6 | C. | x<6 | D. | x≤6 |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
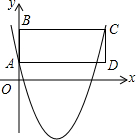 如图,在平面直角坐标系中,抛物线y=ax2-4ax+1(a>0)与y轴交于点A,点D的坐标为($\frac{2}{a}$,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD.
如图,在平面直角坐标系中,抛物线y=ax2-4ax+1(a>0)与y轴交于点A,点D的坐标为($\frac{2}{a}$,1),过点D作DC∥y轴,交抛物线于点C,过点C作CB∥x轴,交y轴于点B,连结AD. 如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度.
如图,已知,AB∥CD∥EF,∠E=140°,∠A=115°,则∠ACE=25度.