题目内容
7.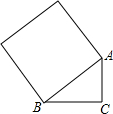 如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25.
如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25.
分析 根据勾股定理求出AB,根据正方形的面积公式求出即可.
解答 解:由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以以AB为边长的正方形的面积为52=25,
故答案为:25.
点评 本题考查了勾股定理的应用,能根据勾股定理求出AB的长是解此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
18.方程$\frac{x-3}{4-x}$-1=$\frac{1}{x-4}$的解是( )
| A. | -3 | B. | 3 | C. | 4 | D. | -4 |
15.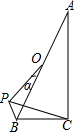 如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
 如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
16. 如图,小正方形的边长均为1,则∠1的正切值为( )
如图,小正方形的边长均为1,则∠1的正切值为( )
 如图,小正方形的边长均为1,则∠1的正切值为( )
如图,小正方形的边长均为1,则∠1的正切值为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
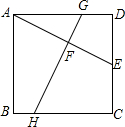 如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G、H,求GF的长,并求$\frac{GF}{GH}$的值.
如图,正方形ABCD中,AB=4,E为BC的中点,F为AE的中点,过点F作GH⊥AE,分别交AB和CD于G、H,求GF的长,并求$\frac{GF}{GH}$的值. 如图,点A(1,4),B(-4,n)在双曲线y=$\frac{k}{x}$的图象上,直线AB分别交x轴、y轴于C,D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF,BE交于点G.
如图,点A(1,4),B(-4,n)在双曲线y=$\frac{k}{x}$的图象上,直线AB分别交x轴、y轴于C,D,过点A作AE⊥x轴,垂足为E,过点B作BF⊥y轴,垂足为F,连接AF,BE交于点G. 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2. 在△ABC中,D,E,F分别是三边上的点,且∠1=∠2,∠C=∠EDF,试求证:DF∥CA,DE∥BC.
在△ABC中,D,E,F分别是三边上的点,且∠1=∠2,∠C=∠EDF,试求证:DF∥CA,DE∥BC.