题目内容
15.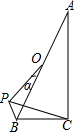 如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为40°或70°或100°.
分析 连结AP,如图,由旋转的性质得OP=OB,则可判断点P、C在以AB为直径的圆上,利用圆周角定理得∠BAP=$\frac{1}{2}$∠BOP=$\frac{1}{2}$α,∠ACP=∠ABP=90°-$\frac{1}{2}$α,∠APC=∠ABC=70°,然后分类讨论:当AP=AC时,∠APC=∠ACP,即90°-$\frac{1}{2}$α=70°;当PA=PC时,∠PAC=∠ACP,即$\frac{1}{2}$α+20°=90°-$\frac{1}{2}$α,;当CP=CA时,∠CAP=∠CAP,即$\frac{1}{2}$α+20°=70°,再分别解关于α的方程即可.
解答 解: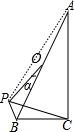 连结AP,如图,
连结AP,如图,
∵点O是AB的中点,
∴OA=OB,
∵OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,
∴OP=OB,
∴点P在以AB为直径的圆上,
∴∠BAP=$\frac{1}{2}$∠BOP=$\frac{1}{2}$α,∠APC=∠ABC=70°,
∵∠ACB=90°,
∴点P、C在以AB为直径的圆上,
∴∠ACP=∠ABP=90°-$\frac{1}{2}$α,∠APC=∠ABC=70°,
当AP=AC时,∠APC=∠ACP,
即90°-$\frac{1}{2}$α=70°,解得α=40°;
当PA=PC时,∠PAC=∠ACP,
即$\frac{1}{2}$α+20°=90°-$\frac{1}{2}$α,解得α=70°;
当CP=CA时,∠CAP=∠CAP,
即$\frac{1}{2}$α+20°=70°,解得α=100°,
综上所述,α的值为40°或70°或100°.
故答案为40°或70°或100°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是用α表示∠ACP和∠CAP,再运用分类讨论的思想和等腰三角形的性质建立关于α的方程.

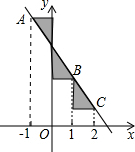 如图,点A、B、C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
如图,点A、B、C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )| A. | 3(m-1) | B. | $\frac{3}{2}(m-2)$ | C. | 1 | D. | 3 |
 如表是我国某城市A区和B区2013年5月至12月的月平均商品住房成交数(单位:套)统计表:
如表是我国某城市A区和B区2013年5月至12月的月平均商品住房成交数(单位:套)统计表:| 月份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A区 | 320 | 315 | 325 | 310 | 315 | 305 | 340 | 315 |
| B区 | 330 | 325 | 315 | 345 | 320 | 315 | 310 | 335 |
(2)A,B两区月平均商品住房成交数差别最大的月份是8月,月平均商品住房成交数差别最小的月份是9月.
| A. | 开口向上 | B. | 当a=2时,经过坐标原点O | ||
| C. | a>0时,对称轴在y轴左侧 | D. | 不论a为何值,都经过定点(1,-2) |
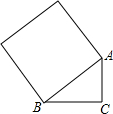 如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25.
如图,∠ACB=90°,AC=3,BC=4,则以AB为边长的正方形面积为25. 如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.
如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.