题目内容
11.先化简,再求值$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$•$\frac{x-y}{x+y}$-$\frac{x}{x-y}$,其中x=tan45°+2sin45°,y=$\sqrt{3}$tan30°-2$\sqrt{2}$cos60°.分析 直接将原式分解因式,进而化简,再把已知代入得出答案.
解答 解:$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$•$\frac{x-y}{x+y}$-$\frac{x}{x-y}$
=$\frac{(x-y)(x+y)}{(x-y)^{2}}$×$\frac{x-y}{x+y}$-$\frac{x}{x-y}$
=-$\frac{x}{x-y}$,
∵x=tan45°+2sin45°=1+$\sqrt{2}$,y=$\sqrt{3}$tan30°-2$\sqrt{2}$cos60°=1-$\sqrt{2}$,
∴原式=-$\frac{1+\sqrt{2}}{1+\sqrt{2}-(1-\sqrt{2})}$=-$\frac{1+\sqrt{2}}{2\sqrt{2}}$=$\frac{-\sqrt{2}-2}{4}$.
点评 此题主要考查了分式的化简求值,正确进行分式的混合运算是解题关键.

练习册系列答案
相关题目
1.下列说法中,错误的是( )
| A. | 两点之间线段最短 | |
| B. | 如果∠α=53°38',那么∠α余角的度数为36°22' | |
| C. | 一个锐角的余角比这个角的补角小90° | |
| D. | 互补的两个角一个是锐角一个是钝角 |
 如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.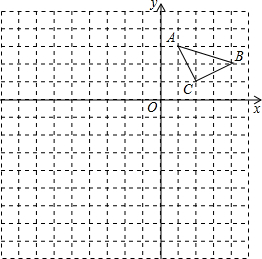 如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
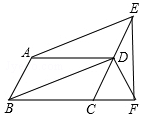 如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD. 尺规作图(不写作法,保留作图痕迹)已知∠AOB的OA边上有一点P,求作⊙O′,使它过点P并且与∠AOB的两边相切.
尺规作图(不写作法,保留作图痕迹)已知∠AOB的OA边上有一点P,求作⊙O′,使它过点P并且与∠AOB的两边相切.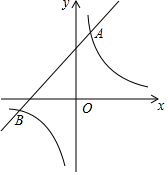 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,且A点的橫坐标为1.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,且A点的橫坐标为1.