题目内容
16.已知直线l1与直线l2:y=$\frac{1}{3}$x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:(1)直线l1的表达式;
(2)直线l1与坐标轴围成的三角形的面积.
分析 (1)由两直线平行可设直线l1的表达式为y=$\frac{1}{3}$x+b,根据点A的坐标,利用待定系数法即可求出直线l1的表达式;
(2)根据一次函数图象上点的坐标特征可求出直线l1与y轴的交点坐标,再根据三角形的面积公式即可求出结论.
解答 解:(1)∵直线l1与直线l2:y=$\frac{1}{3}$x+3平行,
∴设直线l1的表达式为y=$\frac{1}{3}$x+b.
∵直线l1与x轴的交点的坐标为A(2,0),
∴$\frac{1}{3}$×2+b=0,
解得:b=-$\frac{2}{3}$.
∴直线l1的表达式为y=$\frac{1}{3}$x-$\frac{2}{3}$.
(2)当x=0时,y=$\frac{1}{3}$x-$\frac{2}{3}$=-$\frac{2}{3}$,
∴直线l1与y轴的交点坐标为(0,-$\frac{2}{3}$),
∴直线l1与坐标轴围成的三角形的面积S=$\frac{1}{2}$×2×|-$\frac{2}{3}$|=$\frac{2}{3}$.
点评 本题考查了两条直线相交或平行问题、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)由两直线平行设出直线l1的表达式为y=$\frac{1}{3}$x+b;(2)利用一次函数图象上点的坐标特征求出直线l1与y轴的交点坐标.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.张华的身份证号码是320826198309216851,请问张华是( )月出生的?
| A. | 3月 | B. | 6月 | C. | 9月 | D. | 12月 |
1.下列说法中,错误的是( )
| A. | 两点之间线段最短 | |
| B. | 如果∠α=53°38',那么∠α余角的度数为36°22' | |
| C. | 一个锐角的余角比这个角的补角小90° | |
| D. | 互补的两个角一个是锐角一个是钝角 |
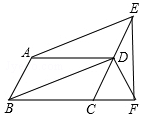 如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,点E、F分别在CD、BC的延长线上,AE∥BD.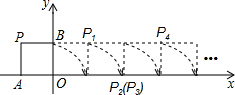 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标x2013=2013.
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3…P2013的位置,则点P2013的横坐标x2013=2013.