题目内容
9.已知非零实数a、b、c满足|a+b+c|+(4a-b+2c)2=0,求$\frac{a+2b}{b-c}$的值.分析 利用非负数的性质列出关系式,用c表示出a与b,代入原式计算即可得到结果.
解答 解:∵|a+b+c|+(4a-b+2c)2=0,
∴$\left\{\begin{array}{l}{a+b=-c}\\{4a-b=-2c}\end{array}\right.$,
解得:a=-$\frac{3}{5}$c,b=-$\frac{2}{5}$c,
则原式=$\frac{-\frac{3}{5}c-\frac{4}{5}c}{-\frac{2}{5}c-c}$=1.
点评 此题考查了分式的值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列方程中,是一元二次方程的是( )
| A. | x2+3x=x(x+1) | B. | a2x+bx+c=0 | C. | x2=0 | D. | x1=0,x2=3 |
4.Rt△ABC与Rt△BAD的斜边重合,D、C位于AB的两侧,现添加一组对应边相等,使△ABC与△BAD全等,下面的添加方法错误的是( )
| A. | AD=AC | B. | BD=BC | C. | AD=BC | D. | AB=BC |
18.给出下列事件
①连续2次抛掷1枚质地均匀的硬币,两次出现“正面朝上”;
②发射一枚炮弹,命中目标;
③在标准大气压下,水在1℃时结冰;
④一个实心铁块丢入水中,铁块浮起.
其中,随机事件的是( )
①连续2次抛掷1枚质地均匀的硬币,两次出现“正面朝上”;
②发射一枚炮弹,命中目标;
③在标准大气压下,水在1℃时结冰;
④一个实心铁块丢入水中,铁块浮起.
其中,随机事件的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (3)(4) |
 如图,E为正方形ABCD边BC延长线上一点,且CE=BD,AE交DC于F,则∠AFC=112.5°.
如图,E为正方形ABCD边BC延长线上一点,且CE=BD,AE交DC于F,则∠AFC=112.5°.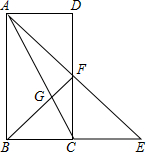 如图,延长矩形ABCD的边BC到E,使CE=BC,连接AE交CD于F点,BF交AC于G,且BG=BC.求矩形两邻边之比AB:BC的值.
如图,延长矩形ABCD的边BC到E,使CE=BC,连接AE交CD于F点,BF交AC于G,且BG=BC.求矩形两邻边之比AB:BC的值.