Question

1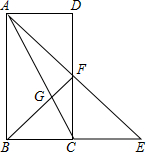．如图，延长矩形ABCD的边BC到E，使CE=BC，连接AE交CD于F点，BF交AC于G，且BG=BC．求矩形两邻边之比AB：BC的值．

Answer 1

分析 先判断出点G是△ABE的重心，得出$\frac{BG}{BF}=\frac{2}{3}$，再利用勾股定理找出a，b的关系，即可求出比值．

解答 解：在矩形ABCD中，CD=AB，AD=BC，∠ECF=∠ADF=90°，
∵BC=CE，
∴CE=AD，
在△ECF和△ADF中，$\left\{\begin{array}{l}{∠CFE=∠DFA}\\{∠ECF=∠ADF=90°}\\{CE=AD}\end{array}\right.$，
∴△ECF≌△ADF
∴AF=EF，CF=DF=$\frac{1}{2}$CD=$\frac{1}{2}$AB，
∵BC=CE，
∴点G是△ABE的重心，
∴$\frac{BG}{GF}=\frac{1}{2}$，
∴$\frac{BG}{BF}=\frac{2}{3}$，
设AB=a，BC=BG=b，
根据勾股定理得，
BF²=BC²+CF²，
∴BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{{b}^{2}+\frac{{a}^{2}}{4}}$，
∴$\frac{b}{\sqrt{{b}^{2}+\frac{{a}^{2}}{4}}}=\frac{2}{3}$，
∴a=$\sqrt{5}$b，
∴$\frac{AB}{BC}=\frac{\sqrt{5}b}{b}=\sqrt{5}$．
即：矩形两邻边之比AB：BC的值为$\sqrt{5}$．

点评 此题是矩形性质，主要考查了三角形的重心及性质，勾股定理，全等三角形的判定和性质，解本题的关键是判断出点G是三角形ABE的重心，也是解本题的难点．