题目内容
15.把长与宽之比为$\sqrt{2}$的矩形纸片称为标准纸.现有一张标准纸,BC=$\sqrt{2}$,AB=1,将这张标准纸按如图,一次又一次对开后,所得的矩形纸片都是标准纸.问第5次对开后所得标准纸的周长为$\frac{2+\sqrt{2}}{4}$,第2014次对开后所得标准纸的周长为$\frac{1+\sqrt{2}}{{2}^{1006}}$.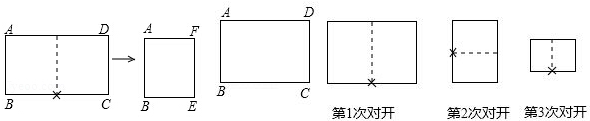
分析 分别求出每一次对折后的周长,进而得出变化规律求出即可.
解答 解:对开第一次,周长为:2(1+$\frac{1}{2}$$\sqrt{2}$)=2+$\sqrt{2}$,
第二次,周长为:2($\frac{1}{2}$+$\frac{\sqrt{2}}{2}$)=1+$\sqrt{2}$,
第三次,周长为:2($\frac{1}{2}$+$\frac{\sqrt{2}}{4}$)=1+$\frac{\sqrt{2}}{2}$,
第四次,周长为:2($\frac{1}{4}$+$\frac{\sqrt{2}}{4}$)=$\frac{1+\sqrt{2}}{2}$,
第五次,周长为:2($\frac{1}{4}$+$\frac{\sqrt{2}}{8}$)=$\frac{2+\sqrt{2}}{4}$,
第六次,周长为:2($\frac{1}{8}$+$\frac{\sqrt{2}}{8}$)=$\frac{1+\sqrt{2}}{4}$,
…
∴第5次对开后所得标准纸的周长是:$\frac{2+\sqrt{2}}{4}$,
第2014次对开后所得标准纸的周长为:$\frac{1+\sqrt{2}}{{2}^{1006}}$.
故答案为:$\frac{2+\sqrt{2}}{4}$,$\frac{1+\sqrt{2}}{{2}^{1006}}$.
点评 此题主要考查了翻折变换性质以及规律性问题应用,根据已知得出对开后所得标准纸的周长变化规律是解题关键.

练习册系列答案
相关题目
6. 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )| A. | OC∥AE | B. | EC=BC | C. | ∠BOC=2∠CAE | D. | AC⊥OE |
3. 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则AD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则AD的长为( )
 如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则AD的长为( )
如图,将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,若CD=8,BE=5,则AD的长为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
20.下列各数中,是负数的是( )
| A. | -(-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$)2 | C. | (-2)3 | D. | (-2)0 |
5.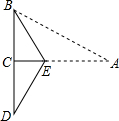 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
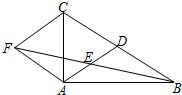 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.