题目内容
16.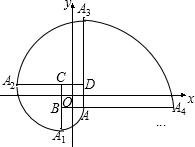 如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).
如图,在直角坐标系中,四边形ABCD是正方形,A(1,-1),B(-1,-1),C(-1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是(1,4031).
分析 先分别求出A1的坐标是(-1,-3),A2的坐标是(-5,1),A3的坐标是(1,7),A4的坐标是(9,-1),从中找出规律,依规律计算即可.
解答 解:从图中可以看出A1的坐标是(-1,-3)
A2的坐标是(-5,1)
A3的坐标是(1,7)
A4的坐标是(9,-1)
2015÷4=503…3
∴点A2015的坐标是A3的坐标循环后的点.
依次循环则A2015的坐标在x轴上的是1,
y轴上的坐标是可以用n=(1+2n)(n为自然数)表示.
那么A2015实际上是当n=2015时的数,所以(1+2×2015)=4031.
A2015的坐标是(1,4031),
故答案为:(1,4031).
点评 本题主要考查了点的坐标的变化规律和对“正方形的渐开线”的理解,发现规律,理解“正方形的渐开线”是解答此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
6. 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{BE}$的中点,则下列结论不成立的是( )| A. | OC∥AE | B. | EC=BC | C. | ∠BOC=2∠CAE | D. | AC⊥OE |
11.下列各图案中,是由一个基本图形通过平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
8.若|a|=2,|b|=5,则|a-b|的值等于( )
| A. | 3 | B. | 7 | C. | -7 | D. | 3或7 |
5.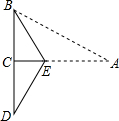 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
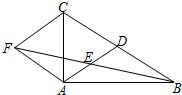 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.