题目内容
3.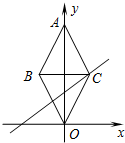 如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,则菱形ABOC的面积是4.
如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,则菱形ABOC的面积是4.
分析 首先设OA与BC相较于点D,由四边形ABOC是菱形,可求得点C的纵坐标,又由直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,可求得点C的坐标,继而求得BC的长,则可求得答案.
解答  解:设OA与BC相较于点D,
解:设OA与BC相较于点D,
∵四边形ABOC是菱形,
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$×4=2,OA⊥BC,
则点C的纵坐标为2,
∵直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,
∴$\frac{2}{3}x+\frac{4}{3}$=2,
解得:x=1,
∴点C的坐标为:(1,2),
∴BC=2,
∴S菱形ABOC=$\frac{1}{2}$OA•BC=$\frac{1}{2}$×4×2=4.
故答案为:4.
点评 此题考查了菱形的性质以及一次函数的性质.注意求得点C的坐标是解此题的关键.

练习册系列答案
相关题目
18.下列各式是一元二次方程的是( )
| A. | x2+5x-3=0 | B. | $\frac{3}{x}+{x}^{2}$-1=0 | C. | x2+5xy-y2=0 | D. | 4x-1=0 |
8.某日中午,太姥山风景名胜区气温由早晨的-3℃,上升了8℃,这天中午的气温是( )
| A. | -11℃ | B. | 11℃ | C. | 5℃ | D. | -5℃ |
13. 已知a,b,c是三个有理数,他们在数轴上的位置如图所示,化简|a-b|+|c-a|-|b+c|得( )
已知a,b,c是三个有理数,他们在数轴上的位置如图所示,化简|a-b|+|c-a|-|b+c|得( )
 已知a,b,c是三个有理数,他们在数轴上的位置如图所示,化简|a-b|+|c-a|-|b+c|得( )
已知a,b,c是三个有理数,他们在数轴上的位置如图所示,化简|a-b|+|c-a|-|b+c|得( )| A. | 2c-2b | B. | -2a | C. | 2a | D. | -2b |
 如图,在⊙O中,∠ACB=∠D=60°,AC=4,求△ABC的周长.
如图,在⊙O中,∠ACB=∠D=60°,AC=4,求△ABC的周长.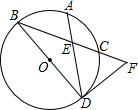 如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.
如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.