题目内容
12.若两个一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0),则称函数y=(k1+k2)x+b1b2为这两个函数的“和谐函数”.(1)求一次函数y=2x+3与y=-4x+4的“和谐函数”的表达式,若此“和谐函数”与x轴相交于点A,与y轴相交于点B,求△ABO的面积;
(2)若一次函数y=-ax+1,y=x-2b的“和谐函数”为y=4x+3,则a=-3,b=-$\frac{3}{2}$;
(3)已知一次函数y=x+b与y=-kx+5的“和谐函数”的图象经过第一、二、四象限,则常数k、b满足的条件为:k>1且b>0(用“>”、“=”、“<”填空).
分析 (1)根据和谐函数的定义即可直接求解;
(2)根据和谐函数定义即可得到一个关于a和b的方程组,解方程组求解;
(3)首先求得和谐函数,然后根据图象经过第一、二、四象限,即可列不等式求解.
解答 解:(1)此“和谐函数”是y=(2-4)x+3×4,即y=-2x+12,
令x=0,则y=12,
当y=0时,-2x-12=0,解得:x=6,
则S△ABO=$\frac{1}{2}$×6×12=36;
(2)根据题意得:$\left\{\begin{array}{l}{-a+1=4}\\{-2b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=-\frac{3}{2}}\end{array}\right.$.
故答案是:-3,-$\frac{3}{2}$;
(3)根据题意得:$\left\{\begin{array}{l}{1-k<0}\\{5b>0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k>1}\\{b>0}\end{array}\right.$.
故答案是:>,>.
点评 本题考查了一次函数的性质,一次函数中当k>0时,y随x的增大而增大,k<0时,y随x的怎大而减小.理解和谐函数的定义是关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
20.下列的点在第四象限的是( )
| A. | (3,-9) | B. | (2,7) | C. | (-1,6) | D. | (-2,-8) |
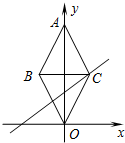 如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,则菱形ABOC的面积是4.
如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线y=$\frac{2}{3}x+\frac{4}{3}$过点C,则菱形ABOC的面积是4.