Question

18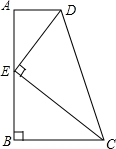．如图，在四边形ABCD中，AD∥BC，∠ABC=90°，E是AB上一点，且DE⊥CE．若AD=1，BC=2，CD=3，则CE与DE的数量关系正确的是（　　）

• A． CE=$\sqrt{3}$DE
• B． CE=$\sqrt{2}$DE
• C． CE=3DE
• D． CE=2DE

Answer 1

分析 过点D作DH⊥BC，利用勾股定理可得AB的长，利用相似三角形的判定定理可得△ADE∽△BEC，设BE=x，由相似三角形的性质可解得x，易得CE，DE 的关系．

解答 解：过点D作DH⊥BC，
∵AD=1，BC=2，
∴CH=1，
DH=AB=$\sqrt{{CD}^{2}{-CH}^{2}}$=$\sqrt{{3}^{2}{-1}^{2}}$=2$\sqrt{2}$，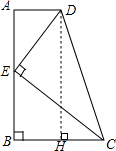
∵AD∥BC，∠ABC=90°，
∴∠A=90°，
∵DE⊥CE，
∴∠AED+∠BEC=90°，
∵∠AED+∠ADE=90°，
∴∠ADE=∠BEC，
∴△ADE∽△BEC，
∴$\frac{AD}{BE}=\frac{AE}{BC}=\frac{DE}{CE}$，
设BE=x，则AE=2$\sqrt{2}-x$，
即$\frac{1}{x}=\frac{2\sqrt{2}-x}{2}$，
解得x=$\sqrt{2}$，
∴$\frac{AD}{BE}=\frac{DE}{CE}=\frac{1}{\sqrt{2}}$，
∴CE=$\sqrt{2}DE$，
故选B．

点评 本题主要考查了相似三角形的性质及判定，构建直角三角形，利用方程思想是解答此题的关键．