题目内容
18.在下面各数中无理数的个数有( )-3.14,$\frac{22}{7}$,0.1010010001,+1.99,-$\frac{π}{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此得出无理数的个数,即可判定选择项.
解答 解:在下面各数中-3.14,$\frac{22}{7}$,0.1010010001,+1.99,-$\frac{π}{3}$,
无理数是-$\frac{π}{3}$,共1个.
故选A.
点评 此题主要考查了无理数的定义,无理数常见的形式有三种(1)开不尽的方根,如$\sqrt{2}$等.(2)特定结构的无限不循环小数,如0.303 003 000 300 003…(两个3之间依次多一个0).(3)含有π的绝大部分数,如2π.注意:判断一个数是否为无理数,不能只看形式,要看化简结果.如$\sqrt{16}$是有理数,而不是无理数.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
8.已知AE,CF是锐角三角形的两条高,AE:CF=2:3,则sinA:sinC=( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |
13.能与4cm,9cm长的两根木棒首尾相接,钉成一个三角形的木棒是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
3.下面关于x的方程中:一元二次方程的个数是( )
①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=$\frac{1}{x}$;④(a2+a+1)x2-a=0.
①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=$\frac{1}{x}$;④(a2+a+1)x2-a=0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.关于旋转的性质,以下说法不正确的是( )
| A. | 对应点到旋转中心的距离相等 | |
| B. | 对应点与旋转中心所连线线段的夹角等于旋转角 | |
| C. | 旋转前、后的图形全等 | |
| D. | 对应点的连线必经过旋转中心且被旋转中心平分 |
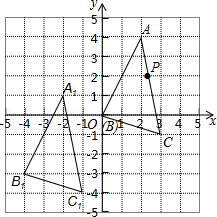 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.