题目内容
13.解方程①x2-7x+6=0
②(5x-1)2=3(5x-1)
③3x2+8x-3=0(用配方法)
④x2-2$\sqrt{2}$x+2=0(用公式法)
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(4)求出b2-4ac的值,再代入公式求出即可.
解答 解:①x2-7x+6=0,
(x-6)(x-1)=0,
x-6=0,x-1=0,
x1=6,x2=1;
②(5x-1)2=3(5x-1),
(5x-1)2-3(5x-1)=0,
(5x-1)(5x-1-3)=0,
5x-1=0,5x-1-3=0,
x1=$\frac{1}{5}$,x2=$\frac{4}{5}$;
③3x2+8x-3=0,
3x2+8x=3,
x2+$\frac{8}{3}$x=1,
x2+$\frac{8}{3}$x+($\frac{4}{3}$)2=1+($\frac{4}{3}$)2,
(x+$\frac{4}{3}$)2=$\frac{25}{9}$,
x+$\frac{4}{3}$=±$\frac{5}{3}$,
x1=$\frac{1}{3}$,x2=-3;
④x2-2$\sqrt{2}$x+2=0,
b2-4ac=(2$\sqrt{2}$)2-4×1×2=0,
x=$\frac{2\sqrt{2}±\sqrt{0}}{2}$,
x1=$\sqrt{2}$,x2=$\sqrt{2}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下面关于x的方程中:一元二次方程的个数是( )
①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=$\frac{1}{x}$;④(a2+a+1)x2-a=0.
①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=$\frac{1}{x}$;④(a2+a+1)x2-a=0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.体育课上,全班男同学进行了100米测验,达标成绩为15秒,下表是某小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
问:(1)这个小组男生的达标率为多少?
(2)这个小组男生的平均成绩是多少秒?
| -0.87 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
(2)这个小组男生的平均成绩是多少秒?
1.若点P(b-3,-2b)在y轴上,则点P的坐标为( )
| A. | (0,-6) | B. | (-6,0) | C. | (0,6) | D. | (6,0) |
18.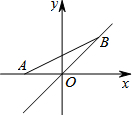 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
2.已知在线段上依次添加1点,2点,3点,…,原线段上所成线段的总条数如表.
若在原线段上添加n个点,则原线段上所有线段总条数为( )
| 图形 |  |  |  |  |
| 线段总条数 | 3 | 6 | 10 | 15 |
| A. | n+2 | B. | 1+2+3+…+n+n+1 | C. | n+1 | D. | $\frac{n(n+1)}{2}$ |
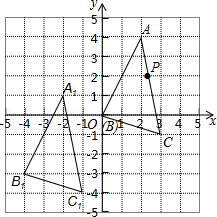 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.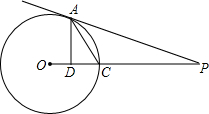 如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD.
如图,PA是⊙O的切线,A为切点,PO交⊙O于D,AD⊥PO于点D,求证:∠PAC=∠CAD. 求证:全等三角形对应边上的高线相等.
求证:全等三角形对应边上的高线相等.