题目内容
12．
如图所示，AB∥CD，∠E=26°，∠C=58°，则∠EAB的度数为（ ）| A． | 84° | B． | 82° | C． | 79° | D． | 96° |
分析 首先延长BA交CE于F，由AB∥CD，根据两直线平行，同位角相等，即可求得∠1的度数，又由三角形外角的性质，可求得∠EAB的度数．
解答 解：延长BA交CE于F，
∵AB∥CD，∠C=58°，
∴∠1=∠C=58°，
∵∠E=26°，
∴∠EAB=∠1+∠E=58°+26°=84°．
故选A．
点评 此题考查了平行线的性质与三角形外角的性质．此题比较简单，解题的关键是注意掌握两直线平行，同位角相等定理的应用．
练习册系列答案
相关题目
如图所示，DE是△ABC的中位线，则△ADE与△ABC的周长比为1：2．
20．下列分式中是最简分式的是（ ）
| A． | $\frac{x-1}{{{x^2}-1}}$ | B． | $\frac{4}{2x}$ | C． | $\frac{2x}{{{x^2}-1}}$ | D． | $\frac{1-x}{x-1}$ |
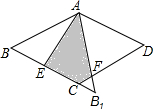如图，在边长为$\sqrt{2}$的菱形ABCD中，∠B=45°，AE是BC边上的高，将△AEB沿AE所在直线翻折得△AEB1，则△AEB1与四边形AECF重叠部分的面积为$\sqrt{2}$-1．
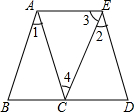已知：如图所示，∠1=∠2，∠3=∠B，AC∥DE，且B，C，D在一条直线上．求证：AE∥BD．
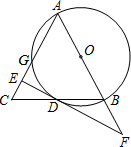如图，以△ABC的边AB为直径的⊙O与BC、AC分别交于D，G，过D的切线垂直AC于E，与AB的延长线交于F．