题目内容
19.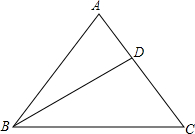 如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数.
如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数.
分析 设∠BDC=x°,由等腰三角形及外角的性质△ABC和△ABD中由三角形内角和定理可表示出∠ABD,可列出方程,求得出答案.
解答 解:∵∠ABC=∠DCB,∠A=∠ADB,
设∠BDC=x°,
则∠C=180°-∠BDC-∠DBC=180°-x°-30°=150°-x°,
∴∠ABC=150°-x°,
∴∠ABD=∠ABC-∠DBC=150°-x°-30°=120°-x°,
在△ABD中,∠A=∠ADB=180°-∠BDC=180°-x°,
∴∠ABD=180°-2(180°-x°)=2x°-180°,
∴120-x=2x-180,
解得x=100,
即∠BDC=100°.
点评 本题主要考查等腰三角形的性质,掌握等边对等角及三角形内角和为180°是解题的关键,注意方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,C为BE上一点.点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
如图,C为BE上一点.点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
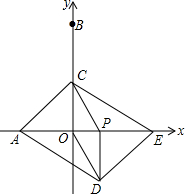 如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.