题目内容
19. 如图,C为BE上一点.点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
如图,C为BE上一点.点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
分析 首先利用平行线的性质可得∠B=∠E,再利用SAS定理判定△ABC≌△CED即可.
解答 证明:∵AB∥ED,
∴∠B=∠E,
在△ABC和△ECD中,
$\left\{\begin{array}{l}{AB=CE}\\{∠B=∠E}\\{BC=ED}\end{array}\right.$,
∴△ABC≌△CED(SAS).
点评 此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
10.若$\frac{a}{b}>0$,$\frac{c}{b}<0$,则ac( )
| A. | 大于0 | B. | 小于0 | C. | 不一定 | D. | 等于0 |
11.下列说法中正确的是( )
| A. | 比正数小的数一定都是负数 | |
| B. | 几个负数相加,和一定是负数 | |
| C. | 减去一个负数,等于加上一个非负数 | |
| D. | 两个负数相减,差一定是负数 |
 如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.
如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理. 如图,MN与PQ相交于点O,MP=MQ,NP=NQ,求证:OP=OQ,PQ⊥MN.
如图,MN与PQ相交于点O,MP=MQ,NP=NQ,求证:OP=OQ,PQ⊥MN.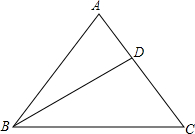 如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数.
如图,△ABC中,∠ABC=∠C,点D是AC边上一点,∠A=∠ADB,∠DBC=30°,求∠BDC的度数.