题目内容
8.西南铝业集团成功研制出一种新型镍合金产品.批量生产后向A、B两地销售,市场火爆得供不应求.已知这种产品每月的产量x(吨)与成本y(万元)成二次函数关系:y=$\frac{1}{10}$x2+5x+90,在A、B两地每吨的售价PA(万元)和PB(万元)均与x成一次函数.(1)已知PA=-$\frac{1}{20}$x+14,若每月的产量x(吨)都在A地销售,请你用含x的代数式表示在A地每月的销售额,并求利润WA(万元)与x之间的函数关系式(注;利润=销售额-成本)
(2)若PB=-$\frac{1}{10}$x+b(b为常数),如果每月的产量x(吨)都在B地销售,可获得的最大利润为35万元,求b的值;
(3)铝业集团2014年2月计划生产并销售该产品18吨,根据(1),(2)中的结果请你通过计算并选择在A地还是在B地销售才能获得较大的利润?
分析 (1)依据年利润=年销售额-全部费用即可求得利润WA(万元)与x之间的函数关系式;
(2)求出利润WB(万元)与x之间的函数关系式,根据最大年利润为35万元.求出b的值;
(3)分别求出x=18时,WA和WB的值,通过比较WA和WB大小就可以帮助投资商做出选择.
解答 解:(1)A地当年的年销售额为(-$\frac{1}{20}$x+14)•x=(-$\frac{1}{20}$x2+14x)万元;
wA=(-$\frac{1}{20}$x2+14x)-($\frac{1}{10}$x2+5x+90)=-$\frac{3}{20}$x2+9x-90.
(2)在B地区生产并销售时,
年利润:wB=-$\frac{1}{10}$x+b-($\frac{1}{10}$x2+5x+90)
=-$\frac{1}{5}$x2+(b-5)x-90.
由$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{5})×(-90)-(n-5)^{2}}{4×(-\frac{1}{5})}$=35,
解得b=15或-5.
经检验,b=-5不合题意,舍去,
∴b=15.
(3)在乙地区生产并销售时,年利润
wB=-$\frac{1}{5}$x2+10x-90,
将x=18代入上式,得wB=25.2(万元);
将x=18代入wA=-$\frac{3}{20}$x2+9x-90,
得wA=23.4(万元).
∵WB>WA,
∴应选B地.
点评 本题考查了二次函数的应用,本题是一道最佳方案选择题,通过计算、比较同一个自变量的两个函数值的大小来选择最佳方案.依据年利润=年销售额-全部费用即可求得利润WA(万元)与x之间的函数关系式及利润WB(万元)与x之间的函数关系式,分别求出x=18时,WA和WB的值,通过比较WA和WB大小就可以帮助投资商做出选择

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案| A. | $\sqrt{20x}$ | B. | $\sqrt{7{a^2}}b$ | C. | $\sqrt{{a^2}-{b^2}}$ | D. | $\sqrt{\frac{a}{3}}$ |
| A. | 任何一个有理数的绝对值都是正数 | |
| B. | 有理数可以分为正有理数,负有理数和零 | |
| C. | 两个有理数和为正数,这两个数不可能都为负数 | |
| D. | 0既不是正数也不是负数 |
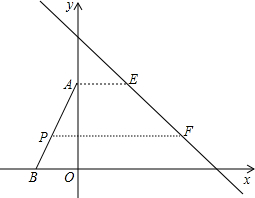 如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.
如图,△ABO的顶点A、B的坐标分别为(0,4)、(-2,0),直线l交x轴于C、交y轴于D,且它所对应的函数表达式为y=-x+6;规定:对于平面上的某一点M,当它沿水平向右的方向平移,平移到直线l上为止,这个过程中平移的距离,称为点M的“右平移距离”.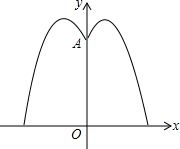 某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题:
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个柱子0A,0恰在水面中心,安装在柱子顶端A处的两个旋转喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过0A的任意平面上,抛物线形状如图所示,建立平面直角坐标系,右边-条抛物线水流喷出的高度y(m)与水面距离x(m)之间的关系式是y=-x2+2x+$\frac{7}{2}$.请回答下列问题: 如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,求EC的长.
如图,在?ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,求EC的长.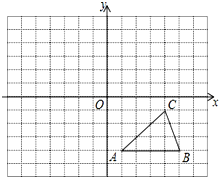 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(-4,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(-4,1).