题目内容
9.解方程:(1)$\frac{1}{x-2}+3=\frac{1-x}{2-x}$;
(2)$\frac{x}{x-1}-\frac{2x-1}{{{x^2}-1}}=1$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:1+3x-6=x-1,
移项合并得:2x=4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:x(x+1)-2x+1=x2-1,
解得:x=2,
经检验x=2是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
14.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{24}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{{x}^{2}+{y}^{2}}$ |
19.在?ABCD中,下列条件不能判断ABCD是正方形的是( )
| A. | ∠ABC=90°且AB=AD | B. | AB=AC且AC⊥BD | C. | AC⊥BD且AC=BD | D. | AC=BD且AB=BC |
 如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.
如图,直线l1∥l2,∠α=∠β,∠1=35°,则∠2=145°.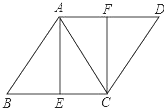 如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF. 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).