��Ŀ����
2��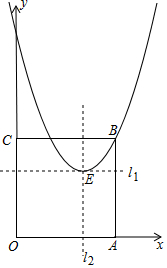 ��ƽ��ֱ������ϵ�У�������OABC�Ķ���B�ڵ�һ���ޣ�����A��C�ֱ���x���y���ϣ�ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E���Ե�EΪ�����������K������B��6��6����
��ƽ��ֱ������ϵ�У�������OABC�Ķ���B�ڵ�һ���ޣ�����A��C�ֱ���x���y���ϣ�ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E���Ե�EΪ�����������K������B��6��6������1����������K�Ľ���ʽ��
��2����P���߶�OC��һ�㣬��O����AP�ĶԳƵ�ΪM��
������M����ֱ��l1��l2��ʱ�������������»�����ƽ�ƶ��٣�ʹ�䶥������AM�ϣ�
������M�����������ϣ���ֱ��д��һ����������ĵ�P�����꣮
���� ��1�����ô���ϵ�������ɽ�����⣻
��2������AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2����M1��m��4����M2��4��n�������m��n���ɽ�����⣮�ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
��� 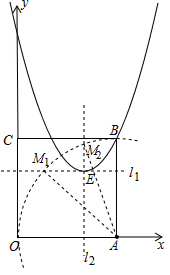 �⣺��1����ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E��
�⣺��1����ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E��
���E��������4��4����
��������K�Ľ���ʽΪy=a��x-4��2+4��
��������K������B��6��6����
��6=a��6-4��2+4��
��ã�a=$\frac{1}{2}$��
��������K�Ľ���ʽΪy=$\frac{1}{2}$��x-4��2+4��
��2������AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2��
��M1��m��4����M2��4��n����
��A��6��0����OM=6��
�ࣨm-6��2+42=62����4-6��2+n2=62��
���m=6-2$\sqrt{5}$��n=4$\sqrt{2}$��
��M��6-2$\sqrt{5}$��4����
��$\frac{{h}_{1}}{4}$=$\frac{2}{2\sqrt{5}}$��
��ã�h1=$\frac{4\sqrt{5}}{5}$��
�ཫ����������ƽ��4-$\frac{4\sqrt{5}}{5}$��ʹ�䶥������AM1�ϣ�������������ƽ��4$\sqrt{2}$-4��ʹ�䶥������AM2�ϣ�
�ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
���� ���⿼����κ����뼸�α任�������ε����ʡ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����ò���������⣮

| A�� | ��am��bm����a��b | B�� | ��am2��bm2����a��b | ||
| C�� | ��a��b����am2��bm2 | D�� | ��a��b��ab��0����$\frac{1}{a}$��$\frac{1}{b}$ |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
| A�� | 2 | B�� | 8 | C�� | 15 | D�� | -15 |
| A�� | ˮ�Ǵ��� | B�� | ������� | C�� | ˮ������ | D�� | �����伢 |