题目内容
10.关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=1+m}\\{x-2y=6-3m}\end{array}\right.$,(1)若m与方程组的解中的x或y相等,则m的值为2或5;
(2)若存在一个m的值,使得这个方程组的解x,y为整数,请写出一个m的值,并求出此方程组的解.
分析 (1)先解方程组$\left\{\begin{array}{l}{x+y=1+m}\\{x-2y=6-3m}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{8-m}{3}}\\{y=\frac{4m-5}{3}}\end{array}\right.$,讨论:当x=m时,$\frac{8-m}{3}$=m;当y=m时,$\frac{4m-5}{3}$=m,然后分别解关于m的一次方程即可;
(2)利用(1)中结论易得当m=5时,这个方程组的解x,y为整数,于是得到此方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$.
解答 解:(1)解方程组$\left\{\begin{array}{l}{x+y=1+m}\\{x-2y=6-3m}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{8-m}{3}}\\{y=\frac{4m-5}{3}}\end{array}\right.$,
当x=m时,$\frac{8-m}{3}$=m,解得m=2,
当y=m时,$\frac{4m-5}{3}$=m,解得m=5,
所以当m为2或5时,m与方程组的解中的x或y相等;
故答案为2或5.
(2)当m=5时,这个方程组的解x,y为整数,此方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$.
点评 本题考查了二元一次方程组的解:二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.

练习册系列答案
相关题目
7.某市举行了一次数学竞赛,分段统计参赛同学的成绩,从中抽查了50名学生的成绩如下表:
这次数学竞赛的平均成绩是( )
| 分数段/分 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
| 人数/人 | 5 | 20 | 15 | 10 |
| A. | 81 | B. | 82 | C. | 79 | D. | 75.5 |
 近年来交通事故发生率逐年上升,交通问题成为重大民生问题,鄱阳二中数学兴趣小组为检测汽车的速度设计了如下实验:如图,在公路MN(近似看作直线)旁选取一点C,测得C到公路的距离为30米,再在MN上选取A、B两点,测得∠CAN=30°,∠CBN=60°;
近年来交通事故发生率逐年上升,交通问题成为重大民生问题,鄱阳二中数学兴趣小组为检测汽车的速度设计了如下实验:如图,在公路MN(近似看作直线)旁选取一点C,测得C到公路的距离为30米,再在MN上选取A、B两点,测得∠CAN=30°,∠CBN=60°;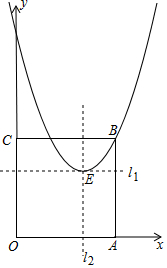 在平面直角坐标系中,正方形OABC的顶点B在第一象限,顶点A、C分别在x轴和y轴上,直线l1:x=4与直线l2:y=4相交于点E,以点E为顶点的抛物线K经过点B(6,6).
在平面直角坐标系中,正方形OABC的顶点B在第一象限,顶点A、C分别在x轴和y轴上,直线l1:x=4与直线l2:y=4相交于点E,以点E为顶点的抛物线K经过点B(6,6).