题目内容
18．
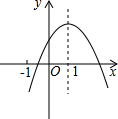二次函数y=ax2+bx+c的图象如图所示，则在下列各不等式中成立的个数是（ ）①abc＜0；②9a+3b+c＜0；③a+c＞b；④2a+b=0；⑤c＞-3a．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
分析 根据开口方向、对称轴、抛物线与y轴的交点，确定a、b、c的符号，根据对称轴和图象确定y＞0或y＜0时，x的范围，确定代数式的符号．
解答 解：①∵开口向下，∴a＜0，对称轴在y轴的右侧，b＞0，抛物线与y轴交于正半轴，c＞0，∴abc＜0∴①正确；
②当x=3时，y＜0，∴9a+3b+c＜0，②正确；
③当x=-1时，y＜0，∴a-b+c＜0，③错误；
④-$\frac{b}{2a}$=1，2a+b=0，④正确；
⑤2a+b=0，a-b+c＜0，∴c＜-3a，⑤错误
故选：B．
点评 本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式．
练习册系列答案
名校课堂系列答案
相关题目
9．经营户小李在水果批发市场上了解到一下信息：
他共用135元钱从市场上批发了苹果和西瓜共50千克到市场上去卖．
（1）请计算小李苹果和西瓜各买了多少千克？
（2）若他能够当天卖完，请问他能赚多少钱？
| 蔬菜品种 | 苹果 | 香蕉 | 西瓜 | 梨子 |
| 批发价（元/千克） | 3.5 | 1.2 | 1.5 | 1.3 |
| 零售价（元/千克） | 4.5 | 1.5 | 2.8 | 1.8 |
（1）请计算小李苹果和西瓜各买了多少千克？
（2）若他能够当天卖完，请问他能赚多少钱？
13．
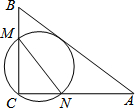如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB，CA分别相交于点M，N，则线段MN长度的最小值是（ ）
如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB，CA分别相交于点M，N，则线段MN长度的最小值是（ ）| A． | $\frac{16}{3}$ | B． | 5 | C． | $\frac{24}{5}$ | D． | $\frac{12}{5}$ |
如图，一山坡的坡比为1：2，某人从山脚下的A点走了500米后到达山顶的点B．那么这人垂直高度上升了100$\sqrt{5}$米．
10．五一黄金周期间，数码产品市场火爆．某商店需要购进一批智能手机和平板电脑共100台，其中智能手机的进货量要超过60台，商店最多可筹集资金345200元．智能手机与平板电脑的进价和售价如下表：
（1）请你帮助商店算一算有多少种进货方案？（不考虑除进价以外的其他费用）
（2）哪种进货方案待商店销售购进的智能手机与平板电脑完后获得利润最多？并求出最大利润．
| 类 别 | 智能手机 | 平板电脑 |
| 进价（元/台） | 3600 | 3200 |
| 售价（元/台） | 4500 | 4000 |
（2）哪种进货方案待商店销售购进的智能手机与平板电脑完后获得利润最多？并求出最大利润．
