题目内容
3.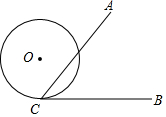 如图,∠ACB=60°,半径为3cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是3$\sqrt{3}$cm.
如图,∠ACB=60°,半径为3cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是3$\sqrt{3}$cm.
分析 设⊙O与CA相切于点P,此时和CB相切于点D,连接OC,OD、OP根据切线长定理得∠OCD=30°,则CD=$\sqrt{3}$OD,求出CD即可解决问题.
解答 解:设⊙O与CA相切于点P,此时和CB相切于点D,连接OC,OD、OP.
∵⊙O与CA相切,⊙O与CB相切,
∴∠OCD=$\frac{1}{2}$∠ACB=30°,
∵OC=OD=3,
∴PD=3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 本题考查切线的性质、切线长定理、30°的直角三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活应用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列计算正确的是( )
| A. | a5-a3=a2 | B. | (-a5)2=a10 | C. | a5•a3=a15 | D. | $\frac{{a}^{6}}{{a}^{3}}$=a2 |
15.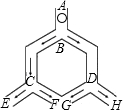 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
13.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共73.若设主干长出x个支干,则可列方程是( )
| A. | (1+x)2=73 | B. | 1+x+x2=73 | C. | (1+x)x=73 | D. | 1+x+2x=73 |