题目内容
2位八年级同学和m位九年级同学一起参加象棋比赛,比赛为单循环,即所有参赛者彼此恰好比赛一场.记分规则是:每场比赛胜者得3分,负者得0分;平局各得1分.比赛结束后,所有同学的得分总和为130分,而且平局数不超过比赛局数的一半,则m的值为 .
考点:一元二次不等式
专题:
分析:首先设平局数为a,胜(负)局数为b,然后根据题意可得2a+3b=130与a+b=
,则可得0≤b=130-(m+1)(m+2)≤43,解此不等式组,即可求得m的值,注意平局数不超过比赛局数的一半,继而可求得答案.
| (m+1)(m+2) |
| 2 |
解答:解:设平局数为a,胜(负)局数为b,
根据题意得:2a+3b=130,
由此得0≤b≤43.
又∵a+b=
,
∴2a+2b=(m+1)(m+2).
∴0≤b=130-(m+1)(m+2)≤43,
即87≤(m+1)(m+2)≤130,
∴m=8或m=9.
当m=8时,b=40,a=5;
当m=9时,b=20,a=35,a>
=
,不合题设.
∴m=8.
故答案为:8.
根据题意得:2a+3b=130,
由此得0≤b≤43.
又∵a+b=
| (m+1)(m+2) |
| 2 |
∴2a+2b=(m+1)(m+2).
∴0≤b=130-(m+1)(m+2)≤43,
即87≤(m+1)(m+2)≤130,
∴m=8或m=9.
当m=8时,b=40,a=5;
当m=9时,b=20,a=35,a>
| a+b |
| 2 |
| 55 |
| 2 |
∴m=8.
故答案为:8.
点评:此题考查了一元二次不等式的应用.此题难度较大,解题的关键是根据题意得到2a+3b=130与a+b=
,继而得到0≤b=130-(m+1)(m+2)≤43.
| (m+1)(m+2) |
| 2 |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
如果一个扇形的圆心角为120°,半径为4cm,则这个扇形的面积为( )cm2.
| A、π | ||
B、
| ||
C、
| ||
D、
|
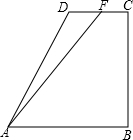 如图,直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=BC,且CD=
如图,直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=BC,且CD=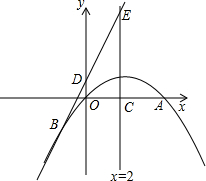 如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.
如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.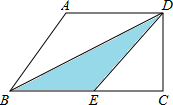 如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合 (如图中的阴影部分).若∠A=120°,AB=4cm,则梯形ABCD的高CD的值为:
如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合 (如图中的阴影部分).若∠A=120°,AB=4cm,则梯形ABCD的高CD的值为: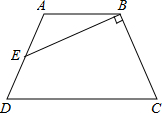 如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是
如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是