题目内容
7. 如图,A,B,C是三个村庄,它们恰好是正方形ABCD的三个顶点,现要在公路BD某处P的附近修建一座农产品收购站.当点P选在何处时AP+BP+CP的值最小?试利用图形的旋转,探索点P的位置.
如图,A,B,C是三个村庄,它们恰好是正方形ABCD的三个顶点,现要在公路BD某处P的附近修建一座农产品收购站.当点P选在何处时AP+BP+CP的值最小?试利用图形的旋转,探索点P的位置.
分析 将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,于是得到△PBP′是等边三角形,根据等边三角形的性质得到PP′=PB,当A′,P′,P,C四点在同一条直线上时,AP+BP+CP的值最小;①将线段BA绕着点B逆时针旋转60°得到BA′,②连接A′C交BD于点P,则点P就是符合条件的点.
解答 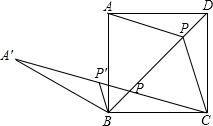 解:如图,将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,
解:如图,将△ABP绕着点B逆时针旋转60°得到△A′BP′,则P′A′=PA,BP=BP′,∠PBP′=60°,
∴△PBP′是等边三角形,
∴PP′=PB,
∴当A′,P′,P,C四点在同一条直线上时,AP+BP+CP的值最小,
综上所述,点P的确定方法是:
①将线段BA绕着点B逆时针旋转60°得到BA′,
②连接A′C交BD于点P,则点P就是符合条件的点.
点评 本题考查了旋转的性质,辅助线的性质,等边三角形的判定和性质,正确的作出图形是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
20. 如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
 如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )
如图,AB∥CD,∠E=120°,∠F=90°,∠A+∠C的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
18. a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )
 a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )| A. | -a-b | B. | a+b | C. | a-b | D. | b-a |
12.已知x>0,且(x-1)2-324=0,则x+1的值为( )
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
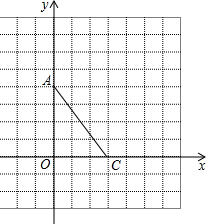 如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.
如图,在直角坐标系中,每个小格子单位长度均为1,点A、C分别在x轴、y轴的格点上.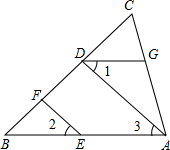 如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.
如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.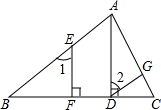 已知:如图,DG∥AB,AD⊥BC于D,EF⊥BC于F,求证:∠1=∠2.
已知:如图,DG∥AB,AD⊥BC于D,EF⊥BC于F,求证:∠1=∠2. 如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.
如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.