题目内容
6．
如图，△ABC中，∠C=90°，三边长分别为a，b，c，⊙O与△ABC的三边均相切，求⊙O的半径r．
分析 证出四边形ODCE为正方形，根据正方形的判定和性质发现直角三角形的内切圆的半径等于它的一条切线长，即可得出结果．
解答 解：设切点分别为D，E，F，连接OD，OE，如图所示：
则OD⊥AC，OE⊥BC．
∵∠C=90°
∴四边形ODCE为正方形，
∴CD=CE=r，AD=AF=b-r，BF=BE=a-r，而AF+BF=c，
∴b-r+a-r=c，
∴r=$\frac{a+b-c}{2}$．
点评 本题考查了三角形的内切圆、切线长定理、正方形的判定与性质；熟练运用切线长定理，能够根据正方形的性质以及切线长定理推导出直角三角形内切圆的半径等于两条直角边的和与斜边的差的一半．
练习册系列答案
名师点拨卷系列答案
相关题目
17．关于x的一元二次方程（m+3）x2+x+m2-9=0有一个根为0，则m的值应为（ ）
| A． | 3 | B． | -3 | C． | 3或-3 | D． | 9 |
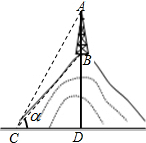如图，在铅直高度为200m的小山上建有一座电视转播塔，某数学兴趣小组为测量电视转播塔的高度，在山脚的C处测得山顶B的仰角为30°（即∠BCD=30°），测得塔顶的仰角为45°（即∠ACD=45°），请根据以上数据求塔高AB．（精确到1m．备用数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．
如图，已知△ABC和过点O的两条互相垂直的直线x、y，画出△ABC关于直线x对称的△A′B′C′，再画出△A′B′C′关于直线y对称的△A″B″C″，观察△ABC与△A″B″C″，这两个三角形具有怎样的对称性？
已知如图，射线OC的端点O在直线AB上，∠AOC的度数比∠BOC度数的2倍多6°，则∠AOC的度数为122°．
如图，点P为等边△ABC外接圆劣弧BC上一点
某服装专卖店老板对第一季度男、女服装的销售收入进行统计，并绘制了扇形统计图（如图）．由于三月份展开促销活动，男女服装的销售收入分别比二月份增长了40%，64%，已知第一季度男女服装的销售总收入为20万元．